Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 76
O eixo de aço é composto por dois segmentos: AC, com diâmetro de 12 mm e CB, com diâmetro de 25 mm. Se estiver preso em suas extremidades A e B e for submetido a um torque de , determine a tensão de cisalhamento máxima no eixo. .
Passo 1
Antes de colocarmos a mão na massa, vamos listar os dados que o enunciado nos deu:
Para nos ajudar, bora fazer o diagrama de corpo livre:
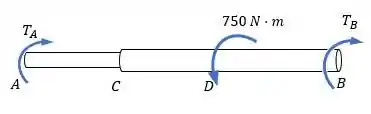
Confiem em mim essa questão é bem tranquila. Vou dar um spoiler do que iremos fazer para matá-la.
Inicialmente, devemos encontrar os valores de e que tendem a equilibrar a torção no eixo. Opa! Falou em “equilíbrio”, então vamos fazer que o somatório de momentos tem que ser igual a zero:
Po, legal, hein. Agora temos uma equação de equilíbrio e duas incógnitas... eu só quero que vocês guardem essa equação, ok? Para acharmos efetivamente os valores de e , como o eixo está engastado em e , utilizaremos o princípio de que o ângulo de torção no trecho é igual ao ângulo de torção no trecho , porém com sentido contrário:
Com o valor de e em mãos e sabendo que , fica fácil determinarmos a tensão de cisalhamento máxima no eixo.
Chega de spoiler! A dica é que vocês tentem fazer a questão depois de entenderem esse passo 1, mas caso não consigam, não tem problema. Vamos resolver passo a passo, beleza?
Então, vamos lá?
Passo 2
Como já foi dito, precisamos encontrar os valores de e que tendem a equilibrar a torção no eixo. Fazendo o somatório de momentos igual a zero e adotando o sentido anti-horário como positivo, temos:
Obs: e são torques de reação que mantém o sistema em equilíbrio, em função do momento torsor aplicado no sistema. Os valores de e também variam em função da distância do ponto onde é aplicado o torque. 😉
Passo 3
Agora, como o eixo está engastado em e , vamos utilizar aquele princípio de que o ângulo de torção no trecho é igual ao ângulo de torção no trecho , porém com sentido contrário.
Atribuindo valores a fórmula, temos:
O e são iguais para todo mundo, então podemos passar o cerol neles, certo?
Guardaram a equação de equilíbrio que eu pedi lá no passo 1? Agora, temos duas equações e duas incógnitas:
Logo será:
Passo 4
Pronto! Já encontramos os valores de , agora vamos utilizar a fórmula da
Como age nos trechos e precisaríamos calcular duas tensões, certo? NÃO!!!! O bizu é ver o trecho que tem o menor diâmetro, nesse caso o trecho :
Agora, calculando para o trecho
Portanto, conclui-se que o valor de no eixo é de .
Executamu mais uma! VAPO!
