Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 116

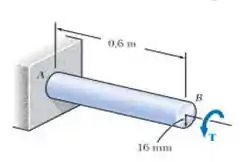
A seção transversal cheia mostrada é feita de aço elastoplástico com T E = 145   M P a   e   G = 77,2   G P a . O torque é aumentado em intensidade até que o eixo tenha sido girado em 6°; em seguida, o torque é removido. Determine (a) a intensidade e a localização da tensão de cisalhamento residual máxima e (b) o ângulo de torção permanente.

Passo 1

E ai gurizada tudo bem? O enunciado pede para que a gente determine (a) a intensidade e a localização da tensão de cisalhamento residual máxima e (b) o ângulo de torção permanente. Temos então os seguintes dados:

c = 0,016   m               φ = 6 ° - 104,712   x   10 - 3 r a d

γ m a x = c φ L = 0,016   x   104,72   x   10 - 3 0,6 = 0,0027925 γ Y = τ Y G = 145   x   10 6 77,2   x   10 9   = 0,0018782 ρ Y c = γ Y γ m a x = 0,0018 0,0027925 = 0,67260 J = π 2 c 4 = π 2   x   0,016 4 = 102,944   x   10 - 9 m 4

O torque é dado por: T Y = J τ Y c = π 2 c 3 τ Y = π 2   x   0,016 3   x   145   x   10 6 = 932,93   N . m

Passo 2

No final do carregamento:

T l o a d = 4 3 T Y   x   1 - 1 4 ρ Y 3 c 3 = 4 3 x   932,93   x   1 - 1 4   x   0,67433 3 = 1,14855   x   10 3 N . m  

Passo 3

Descarregando: elástico T ' = 1,14855   x   10 3 N . m

Em ρ = c , τ ' = T ' c J = 1,14855   x   10 3   x   ( 0,016 ) 102,944   x   10 - 9   = 178,513   x   10 6 P a

Em ρ = ρ Y , τ ' = T ' c J ρ Y c = 178,513   x   10 6   x   0,67433 = 120,376   x   10 6 P a

O ângulo podemos determinar por:

φ = T ' L G J = 1,14855   x   10 3   x   ( 0,6 ) 77,2   x   10 9   x   ( 102,944   x   10 - 9 ) = 86,731   x   10 - 3 r a d = 4,97 °  

Passo 4

Residual: τ r e s = τ l o a d - τ '             φ p e r n = φ l o a d - φ '

  1. Em ρ = c ,     τ r e s = 145   x   10 6 - 178,513   x   10 6 = - 33,513   x   10 6 P a τ r e s = - 33,5   M P a Em ρ = ρ Y , τ r e s = 145   x   10 6 - 120,376   x   10 6 = 24,624   10 6 P a τ r e s = 24,6   M P a

    2. Tensão residual máxima:

  2. φ p e r n = 104,712   x   10 - 3 - 86,731   x   10 - 3 = 17,9990   x   10 - 3 r a d

Resposta

  1. 33,5   M P a     e     ρ = 16,00   m m
  2. φ p e r n = 1,03 °
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolvido o problema 3.55 assumindo que o eixo AB é substituído por um eixo vazado de mesmo diâmetro externo e 25 mm de diâmetro interno.
Uma placa anular de espessura τ e módulo de elasticidade transversal G é utilizada para conectar o eixo AB de raio r 1 ao tubo CD de raio interno r 2 . . Sabendo que é aplicado um torque T á extremida
Dois eixos de seção transversal cheia, feitos de aço G = 77 , 2G P a , são conectados a um disco de acoplamento B e engastados ao suporte rígido em A e C. Para o carregamento mostrado, determine (a) a
(a) Para o eixo de aço com seção transversal cheia mostrado G = 77G P a , determine o ângulo de torção em A. (b) Resolva a parte (a) considerando que o eixo de aço é vazado com 30 mm de diâmetro exter
Determine o ângulo pelo qual a extremidade A gira quando T = 565N ⋅ mm, l = 61 mm, d = 1,59 mm, G=77,2 GPa e n=2 .