Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 83
Um eixo de aço tubular de 1,5 m de comprimento, com diâmetro externo deve ser feito de um aço para o qual e G = 77,2 GPa. Sabendo que o ângulo de torção não deve exceder 4° quando o eixo é submetido a um torque de 600 N/m, determine o maior diâmetro que pode ser especificado no projeto.
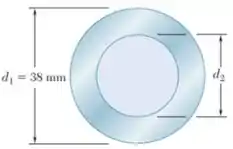
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a frequência mínima na qual o eixo pode girar.
Então podemos determinar o torque a partir da tensão de cisalhamento:
E o torque a partir do ângulo de torção:
Agora vamos usar o menor valor de :
Resposta
Então gurizada, o maior diâmetro do eixo é:
Exercícios de Livros Relacionados
Determinar a máxima tensão de cisalhamento em um eixo maciço de 12m m de diâmetro, que transmite 2,5k W a uma frequência de: a) 25H z
Determinar a máxima tensão de cisalhamento em um eixo maciço de 12m m de diâmetro, que transmite 2,5k W a uma frequência de: b) 50H z
Usando uma tensão de cisalhamento admissível de 50M P a , projetar um eixo maciço de aço para transmitir 15 k W , a uma frequência de:a) 30H z
Usando uma tensão de cisalhamento admissível de 30M P a , projetar um eixo maciço de aço que transmita 1 2 h p , a uma velocidade de:a) 24 00r p m
Usando uma tensão de cisalhamento admissível de 50M P a , projetar um eixo maciço de aço para transmitir 15 k W , a uma frequência de:b) 60H z