Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas de Revisão - Ex. 162

O eixo AB é feito de um material elastoplástico com τ a d m = 12,5   k s i   e   G = 4   x   10 6 p s i . Para o carregamento mostrado, determine (a) o raio do núcleo elástico do eixo, (b) o ângulo de giro do eixo.

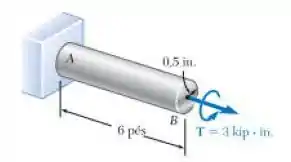
Passo 1

E ai gurizada tudo belezinha? O exercício pede que a gente determine o raio e o ângulo de giro então vem comigo :D. Sabendo que c = 0 , 5   i n .

Entao podemos determinar o torque aplicando na equação abaixo 😉 T Y = J τ Y c = π 2 c 3 τ = π 2   x   0,5 3   x   1.25 = 2,454   k i p . i n .

  1. E também, T = 3 k i p . i n . > T Y     r e g i ã o   p l á s t i c o   c o m   n ú c l e o   e l á s t i c o T = 4 3 T Y   x   1 - 1 4 ρ Y 3 c 3         ∴           ρ Y 3 c 3 = 4 - 3 T T Y = 4 - 3   x   2,454 3 = 0,33307 ρ Y c = 0,69318             ρ Y = 0,69318   x   0,5 = 0,347   i n .
  2. Sabendo que: L = 6 f t = 72   i n .       G = 4   x   10 6   p s i = 4   x   10 3   k s i , podemos determinar o ângulo φ Y = T Y L J G = 2 T Y L π c 4 G = 2   x   2,454   x   72 π   x   0,5 9   x   4   x   10 3 = 0,4499   r a d φ Y φ = ρ Y c           ∴           φ = φ Y ρ Y / c = 0,4499 0,69318 = 0,64904   r a d = 37,2 °

Resposta

a )   0,347   i n . b )   37,2 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo é feito de latão vermelho C83400 e tem seção transversal elíptica. Se for submetido ao carregamento de torção mostrado, determine a tensão de cisalhamento máxima no interior das regiões A C e B
O eixo de aço A-36 é composto por dois segmentos: A C , com diâmetro de 10m m e C B , com diâmetro de 20m m . Se o eixo estiver engastado em suas extremidades A e B e for submetido a um torque distrib
Compare os valores da tensão de cisalhamento elástica máxima e do ângulo de torção desenvolvidos em eixos de aço inoxidável 304 com seções transversais circular e quadrada. Cada eixo tem a mesma área
Os dois eixos de 1m de comprimento são feitos de alumínio 2014 - T 6 . Cada eixo tem diâmetro de 30m m e os dois estão acoplados pelas engrenagens presas a uma das extremidades de cada um deles. As ou
Resolva o Problema 5.89 para a tensão de cisalhamento máxima no interior das regiões A C e B C e ângulo de torção ϕ da extremidade B em relação à C .