Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 26
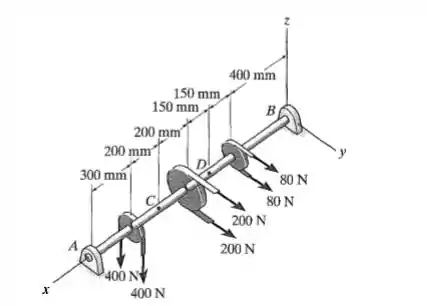
O eixo está apoiado em suas extremidades por dois mancais e e está sujeito às iorças aplicadas às polias nele fixadas. Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto . As forças de agem na direção e as forças de e agem na direção . Os suportes A e B exercem somente as componentes e da força sobre o eixo.
Passo 1
Falaaa! Então, a gente tem uma viga em 3D e quer os esforços internos no ponto . Nesse tipo de questão, quando a gente tem uma viga biapoiada, precisamos começar achando as reações.
Então, vamos achar as reações em e . Mas repara que ele fala que esses suportes só exercem força nos eixos e . Então nossas reações estão só nesses eixos.
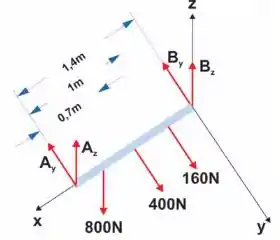
Vamos fazer o diagrama do corpo livre
Passo 2
Agora um momento interessante: eu disse que a gente precisava achar as reações nos suportes. Mas na verdade, a gente só precisa das reações em um dos suportes!
Por que? Cara, a gente quer o esforço interno numa seção. Quando a gente for achar esses esforços, vamos cortar a viga na seção e esquecer que um dos lados existe. Então a gente só precisa de informação sobre um dos lados mesmo.
Vamos usar as equações de momento em para encontrar e . Já que é mais próximo de . Como a gente tem essas forças nos eixos e , temos o somatório de momentos em e , porque elas geram momentos nesses eixos.
Para o momento em relação ao eixo , temos que as forças que geram momento estão em :
Agora para o eixo , as forças que geram momentos estão em . O somatório fica:
Passo 3
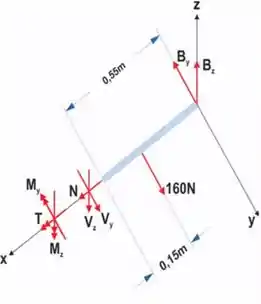
Podemos já analisar os esforços internos. Se a gente pegar a nossa viga, cortar em e olhar só para o lado de , e jogar fora o outro lado, ficamos com o lado onde a gente tem todas informações, certo?
Aí é só colocar as componentes dos esforços internos na seção e descobrir o valor deles pelas equações de equilíbrio.
Mas lembra que como estamos no 3D, temos as componentes e .
Ficamos assim:
Passo 4
Aí é usar as equações de equilíbrio e momento para cada eixo a fim de encontrar o valor dessas componentes.
Começando pelas forças no eixo :
No eixo :
No eixo :
E o somatório dos momentos, começando pelo momento ao redor do eixo :
Momento ao redor do eixo :
E por fim, o momento ao redor do eixo :
Obs: alguns sinais ficaram diferentes do gabarito pela escolha de sentido das componentes no DCL. As duas respostas são válidas visto que nesse capítulo o autor não apresentou ainda a convenção de sinais para esses esforços, ok?