Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 23

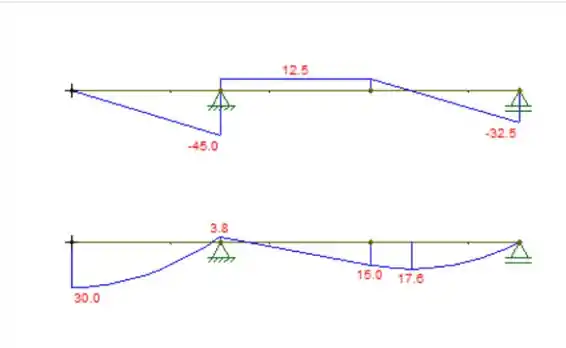
Represente graficamente os diagramas de força cortante e momento fletor para a viga.

Passo 1

Primeiramente, devemos calcular as reações de apoio. Para isso, utilizaremos as equações de equilíbrio:

∑ M a = 0

30 × 1,5 × 0,75 - 30 - 30 × 1,5 × 2,25 + 3 F b = 0

F b = 32,5 k N

∑ F y = 0 → F a + 32,5 - 90 = 0

F a = 57,5 k N

Passo 2

Vamos começar achando as equações do cortante e do momento para as diferentes seções.

Aí é colocar as representações dos esforços com conveção positiva dentro da nossa seção e usar as equações de equilíbrio para cada esforço separadamente..

Nossa origem do eixo x está na ponta esquerda da nossa viga.

Seção OA: 0 ≤ x < 1,5

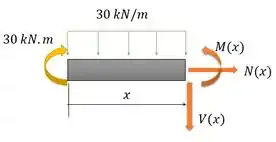
Aí a gente esquece o resto da viga à direita, e foca só nessa parte. Fica assim:

∑ F Y = 0 ⇒ - 30 x - V x = 0

V x = - 30 x

E o somatório de momentos em relação a extremidade direita desse desenhinho:

∑ M = 0 ⇒ - 32,5 x - 30 + 15 x 2 + M x = 0

M x = 32,5 x + 30 - 15 x 2

Passo 3

Seção AC: 1,5 ≤ x ≤ 3

∑ F Y = 0 ⇒ - 1,5 ⋅ 30 + 57,5 - V x = 0

V x = 12,5   k N

∑ M = 0 ⇒ - 30 + 45 ⋅ x - 1,5 2 - 57,5 x - 1,5 + M x = 0

M x = 30 - 45 ⋅ x - 1,5 2 + 57,5 x - 1,5

Passo 4

Seção CB: 3 ≤ x ≤ 4,5

∑ F Y = 0 ⇒ - 1,5 ⋅ 30 + 57,5 - 30 ( x - 3 ) - V x = 0

V x = 12,5 - 30 ( x - 3 )

∑ M = 0 ⇒ - 30 + 45 ⋅ x - 1,5 2 - 57,5 x - 1,5 + 30 x - 3 2 2 + M x = 0

M x = 30 - 45 ⋅ x - 1,5 2 + 57,5 x - 1,5 - 30 x - 3 2 2

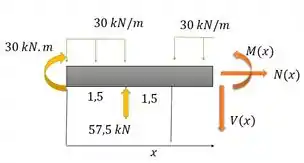
Passo 5

As equações são:

V x = - 30 x   k N 0 ≤ x < 1 ,   5                 12,5   k N   1,5 ≤ x ≤ 3                 12,5 - 30 ( x - 3 )   3 ≤ x ≤ 4,5

M x = 32,5 x + 30 - 15 x 2 0 ≤ x < 1 ,   5                 30 - 45 ⋅ x - 1,5 2 + 57,5 x - 1,5   1,5 ≤ x ≤ 3                 30 - 45 ⋅ x - 1,5 2 + 57,5 x - 1,5 - 30 x - 3 2 2   3 ≤ x ≤ 4,5

Dica: pode cair nessas equações estranhas, mas aí você extrai informações fáceis dela, como onde corta os eixos coordenados, máximo ou mínimo (usando derivada), olhar concavidade da parábola. Aí cê consegue esboçar, bele?

Utilizando as equações podemos traçar os gráficos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga A B é suportada por um pino em A e também por um cabo B C . Um cabo separado C G é usado para manter a estrutura na posição vertical. Se A B pesar2k N / m e o peso da coluna F C for 3k N / m ,
Um dispositivo é usado para suportar uma carga. Se a força aplicada ao cabo for 250 N, determine as tensões T 1 e T 2 em cada extremidade da corrente e, então, represente graficamente os diagramas de
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
Represente graficamente os diagramas de força cortante e momento fletor para o eixo. Os mancais em A e B exercem somente reações verticais no eixo.
Represente graficamente os diagramas de força cortante momento fletor para o eixo. Os mancais em A e D exercem somente reações verticais sobre o eixo. A carga aplicada às polias em B, C e E