Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 28

Determine as cargas internas resultantes que agem na seção transversal da estrutura nos pontos F e G . O contato em E é liso.

Passo 1

Primeiro, vamos fazer o diagrama do corpo livre

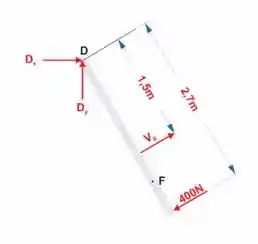
Passo 2

Vamos usar as equações de momento em D   para encontrar V E

∑ M D = 0 V E × 1,5 = 400 × 2,7 V E = 720   N

Passo 3

Agora, vamos analisar a seção em F e usar as equações de momento e equilíbrio.

∑ F x = 0 N F = 0

∑ F y = 0 V F = 400

∑ M F = 0 M F = 400 × 0,6 M F = 240   N . m

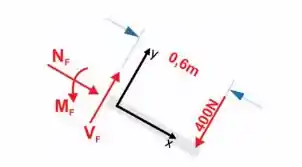
Passo 4

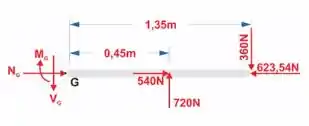
Para a seção G, muda um pouquinho, pois temos que decompor duas forças. Fica assim:

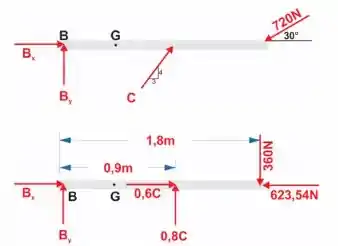
Passo 5

Vamos aplicar a de equilíbrio momento para B para acharmos a força C.

∑ M B = 0 0,8 C × 0,9 = 360 × 1,8 C = 900   N

Passo 6

Por fim, basta utitizar as equações de quilíbrio e momento para a seção em G .

∑ F x = 0 N G + 540 - 623,54 = 0 N G = 83,54

∑ F y = 0 V G - 720 + 360 = 0 V G = 360

∑ M G = 0 M G + 360 × 1,35 = 720 × 0 , 45 M G = 162   N . m

Resposta

N F = 0

V F = 400

M F = 240   N . m

N G = 83,54

V G = 360

M G = 162   N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Represente graficamente os diagramas de força cortante e momento fletor para a viga composta. Os três segmentos estão interligados por pinos em B e E .
Represente graficamente os diagramas de força cortante e momento fletor para a viga e determine a força cortante e momento na viga em função de x , 1,2 mx3m .
A viga está parafusada ou presa por pino em A e repousa sobre um coxim em B que exerce uma carga uniformemente distribuída na viga ao longo de seu 0,6m de comprimento. Represente graficamente os diagr
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
A viga composta consiste em dois segmentos interligados por um pino em B . Represente graficamente os diagramas de força cortante e momento fletor se ela suportar a carga distribuída mostrada na figur