Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 29
A haste do parafuso está sujeita a uma tensão de 400 N. Determine as cargas internas resultantes que agem na seção transversal no ponto C.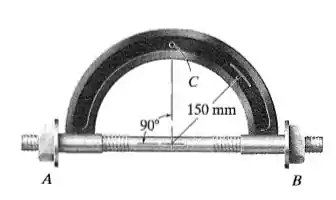
Passo 1
Fala aí galerinha. Bora pra mais uma questão. A gente precisa dos esforços internos em . A ideia para achar esforços internos em uma seção é que a gente pode cortar nossa haste nessa seção e escolher um dos pedaços.
Ele diz que o parafuso sofre uma tensão de . Então, se a gente cortar ele, essa tensão aparece. Esse é a carga interna em todo o parafuso. E o interessante é que se a gente cortar a haste, quem aparece? Os esforços internos nela!
Então, se a gente cortar os dois ao mesmo tempo, e escolher o lado da esquerda, por exemplo, podemos achar os esforços internos em . Olha como fica num DCL:
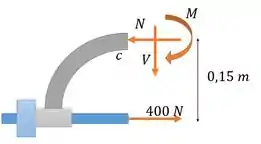
Repara que colocamos as componentes dos esforços internos na seção C. Aí achamos seus valores pelas equações de equilíbrio, ok?
Bora!
Passo 2
Aí a gente aplica aqui as equações de equilíbrio para essa situaçãozinha:
Obs: alguns sinais ficaram diferentes do gabarito pela escolha de sentido das componentes no DCL. As duas respostas são válidas visto que nesse capítulo o autor não apresentou ainda a convenção de sinais para essas cargas, ok?