Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 29
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
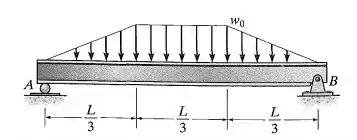
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat. A gente precisa fazer os diagramas de esforços solicitantes para essa viga. Só seguir esse passo a passo que vou mostrar.
Primeiro, vamos determinar as reações de apoio em função do carregamento. Repara que nossa viga e a distribuição nela é simétrica. Então as reações serão iguais.
Para determinarmos as forças de reação, precisamos encontrar primeiro a resultante do carregamento . Ela é dada pela área da figura em que as cargas atuam, neste caso, um trapézio, logo:
Pela simetria:
Bora!
Passo 2
Vamos dividir nossa viga em seções. Nossos pontos críticos serão onde a carga distribuída muda de forma. Teremos então três seções.
Para cada intervalo, a gente corta a viga numa seção genérica, distanciada da origem estabelecida por nós mesmos.
O próximo passo é achar as equações do momento para as diferentes seções. Aí é colocar as representações dos esforços com convenção positiva dentro da nossa seção e usar as equações de equilíbrio para achar os valores desses esforços.
Agora, vamos para a análise dos esforços internos. Na seção 1, , temos:
Vamos achar esse por semelhança de triângulos:
Aí a gente acha o momento pelas equações de equilíbrio:
Ao derivarmos, vamos encontrar a equação para a força cortante. Temos
Passo 3
Já para a seção 2,
Vamos fazer a mesma coisa. Achar e derivar.
Passo 4
Como nosso carregamento é simétrico, não precisamos achar as equações da terceira seção. Para achar o diagrama nelas, na hora de desenhar o cortante, a gente espelha em relação a medade do diagrama e em relação ao eixo . E o momento a gente espelha em torno da metade somente.
Às vezes as equações ficam feias, mas para esboçar, você pode achar alguns pontos chave (onde as curvas cortam os eixos coordenados e nos extremos das seções), os valores máximos e mínimos, e se ligar no tipo de curva que precisa fazer.
Por fim, podemos esboçar os diagramas para momento fletor e força cortante. Fica assim:
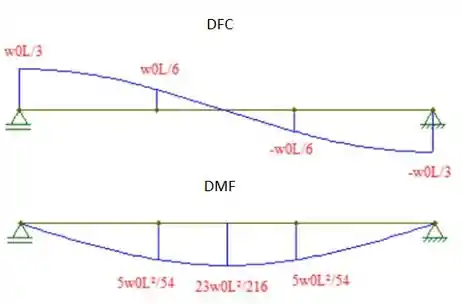
Onde os pontos são valores de máximo e mínimo da funções.
Resposta
