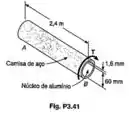
Para o eixo composto do Prob. 3.41, as tensões de cisalhamento admissíveis são conhecidas como sendo na camisa de aço e no núcleo de alumínio. Determinar: (a) o maior torque que pode ser aplicado ao eixo; (b) o correspondente ângulo de torção em B.

Essa é uma situação estaticamente indeterminada! Não sabemos a quantidade de torque que atua em cada material. Então, como podemos calcular o torque?

Bem, sabemos que a camisa de aço é colada no núcleo de alumínio. Isso quer dizer que os dois materiais têm a mesmo ângulo de torção . E a gente já sabe fórmula do ângulo de torção:

Como a gente já conhece os valores de e , a gente pode usar o ângulo de torção para descobrir os torques desconhecidos.

Primeiro calculamos o ângulo de torção na Luva de aço:

E depois no núcleo de alumínio:

E agora a gente pode igualar:

Para isso, podemos isolar o

Podemos cortar o em cima e embaixo:

E aplicamos os valores conhecidos:

Chegamos numa relação entre os torques.

Beleza, a gente relacionou os torques! Mas e agora?

Bom, a gente já conhece as tensões admissíveis em cada material. Vamos calcular o maior torque admissível em cada material.

O maior torque que o alumínio aguenta ocorre quando a tensão no alumínio é igual a tensão admissível:

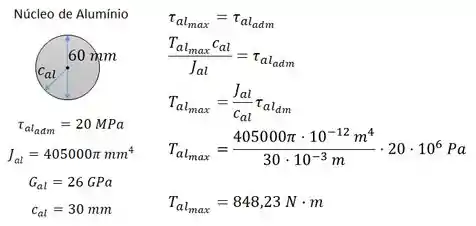
E o maior torque possível no aço acontece quando a tensão no aço for igual a tensão admissível:

Agora já temos tudo que precisamos. Mas precisamos testar duas situações:

HIPÓTESE 1 – O TORQUE NO ALÚMINIO É MÁXIMO:

E agora podemos usar a relação calculada para determinar o torque na Camisa de Aço:

O torque calculado no aço supera o torque admissível no aço. Então essa hipótese está incorreta! Vamos testar outra hipótese

HIPÓTESE 2 – O TORQUE NO AÇO É MÁXIMO

E agora podemos usar a relação calculada para determinar o torque na Camisa de Aço:

Nessa situação, ambos os torques estão dentro dos limites. Ou seja, o torque em cada material é:

Agora que temos o torque em cada material, podemos calcular o torque total: