Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 48

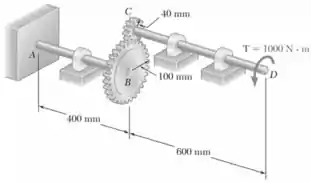
O projeto do sistema de engrenagens e eixo mostrado na figura requer que sejam utilizados eixos de aço de mesmo diâmetro para AB e CD. E necessário também que τ a d m ≤ 60   M P a   e que o ângulo ϕ D pelo qual a extremidade D de eixo CD gira e não exceda 1,5°. Sabendo que G = 77,2 GPa, determine o diâmetro necessário para os eixos.

Passo 1

E ai gurizada tudo belezinha? Começamos por pegar alguns dados para os cálculos, para, determinarmos o diâmetro necessário para os eixos

T C D = T D = 1000   N ⋅ m T A B = r B r C T C D = 100 40 1000 = 2500   N ⋅ m

Para o projeto, usaremos o maior torque:

τ = T c J = 2 T π c 3

Isolando c 3

c 3 = 2 T π τ

c 3 = 2 2500 π 60 × 10 6 = 26,526 × 10 - 6   m 3

c = 29,82 × 10 - 3 = 29.82   m m

d = 2 c = 59.6   m m

Agora galerinha, usaremos o ângulo de rotação:

φ D = 1.5 ° = 26.18 × 10 - 3 r a d

Passo 2

No eixo Ab temos os seguintes dados T A B = 2500   N ⋅ m L = 0,4   m

φ A B = T L G J = 2500 0.4 G J = 1000 G J

E n g r e n a g e n s   φ B = φ A B = 1000 G J   φ C = r B r C φ B = 100 40 1000 G J = 2500 G J  

No eixo CD temos os seguintes dados T C D = 1000   N ∙ m e L = 0 ,   6   M

φ C D = T L G J = 1000 0.6 G J = 600 G J

φ D = φ C + φ C D = 2500 G J + 600 G J = 3100 G J = 3100 G π 2 c 4

c 4 = 2 3100 π G φ D = 2 3100 π 77,2 × 10 9 26,18 × 10 - 3 = 976,46 × 10 - 9 m 4

c = 31,435 × 10 - 3   m = 31,435   m m

d = 2 c = 62,9   m m

Devemos usar o maior valor para D: d = 62,9   m m

Resposta

Então gente, o diâmetro dos eixos é: d = 62.9   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um torque de 36 - k i p * m é aplicado a uma cantoneira de aço com abas iguais, de seção transversal L 8x8x1 , e com 10 pés de comprimento. No Apêndice C, verificamos que a espessura da seção é de 1 i
Um torque de intensidade T = 2k i p * i n . é aplicada a cada uma das barras de alumínio mostradas. Sabendo que τ a d m = 6k s i , determine a dimensão b para cada barra.
Uma barra de aço com 4m de comprimento tem uma seção transversal W 310x60 . Sabendo que G = 77,2G P a e que a tensão de cisalhamento admissível é de 40 MPa, determine (a) o maior torque T que pode ser
Uma barra de aço com 2438 mm de comprimento e seção transversal W 200x4,61 está submetida a um torque de 565N * m . As propriedades da seção laminada são dadas no Apêndice C. Sabendo que G = 77,2G P a
No sistema de engrenagens cônicas mostrado, α = 18,43 ° . Sabendo que a tensão de cisalhamento admissível é de 8 ksi em cada eixo e que o sistema está em equilíbrio, determine o maior torque de T A qu