Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 47

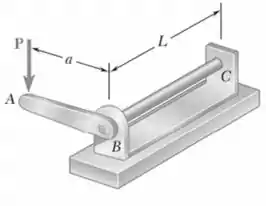
A haste cilíndrica cheia BC de comprimento L = 24   i n . é conectada na alavanca rígida AB de comprimento a = 15   i n , e no suporte C. Especificações de projeto exigem que o deslocamento de A não exceda 1 in, quando uma força P de 100 lb é aplicada em A. Para o material indicado, determine o diâmetro da haste necessário.

Alumínio: τ a l l = 10   k s i , G = 3,9 × 10 6   p s i

Passo 1

Então pessoal para podermos determinar necessário para haste precisamos seguir as seguintes etapas começando primeiramente pelo ângulo de torção permitido, pois precisaremos dele para os demais cálculos:

s e n ϕ = Δ a = 1 5 =   0.06667

ϕ = 3.8226 ° = 0.066716   r a d

A torção é determinada por:

T = P a   c o s   ϕ   = 100 15 c o s 3.8226 ° = 1496.7   l b / i n  

Agora precisamos determinar as medidas nos baseando na torção e na tensão da haste:

Baseado na torção temos

ϕ = T L G J = 2 T L π G c 4

Isolando c 4 temos:

c 4 = 2 T L π G ϕ

c 4 = 2 1496,7 24 π 3,9 × 10 6 0,066716 = 87,888 × 10 - 3 i n 4 = 0,544   i n

Passo 2

Baseado na tensão

  τ = T c J = 2 T π c 3

Isolando c 3 temos:

c 3 = 2 T π τ         10,000   p s i

  c 3 = 2 1496.7 π 10,000 = 95,283 × 10 - 3 i n 3 = 0,457   i n

Agora calculamos para encontrarmos o maior diâmetro da haste

c t o = 0,544   i n d = 2 c t o = 2 0,544 = 1,089   i n

c t e = 0,457   i n d = 2 c t o = 2 0,457 = 0,914   i n

Resposta

Então gurizada, com um pouco de trabalho conseguimos determinar o diâmetro da haste baseado no maior esforço da peça, o diâmetro deve ser 1,089   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas barras são feitas no mesmo material. A seção transversal da barra A é um quadrado de lado b e a seção transversal da barra B é um círculo de diâmetro b. Sabendo que as barras estão submetidas ao
Os eixos A e B são feitos do mesmo material e têm mesmo comprimento e área de seção transversal, mas A tem seção transversal circular e B tem seção transversal quadrada. Determine a razão entre os máx
Os eixos A e B são feitos do mesmo material e têm mesmo comprimento e área de seção transversal, mas A tem seção transversal circular e B tem seção transversal quadrada. Determine a relação dos valore
Uma cantoneira de aço com 1,25 m de comprimento tem seção L 127x76x6,4m m . Obtém-se do Apêndice C que sua espessura é de 64 mm e que a área de sua transversal é 1250 mm². Sabendo que τ a d m = 60M P
Um torque de intensidade T = 300N * m é aplicado a cada uma das barras de alumínio mostradas τ a d m = 60M P a , determine a dimensão b para cada barra.