Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 46
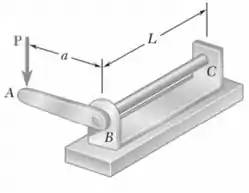
A haste cilíndrica cheia BC de comprimento . é conectada na alavanca rígida AB de comprimento , e no suporte C. Especificações de projeto exigem que o deslocamento de A não exceda 1 in, quando uma força P de 100 lb é aplicada em A. Para o material indicado, determine o diâmetro da haste necessário.
aço: ,
Passo 1
E ai gurizada tudo belezinha? O enunciado pede para que a gente determine o diâmetro da haste necessário. Muito bem, vamos começar:
Primeiramente vamos determinar o angulo de torção:
Assim podemos encontrar a torção do elemento
Com base na torção:
Isolando temos:
Passo 2
Com base na tensão de cisalhamento temos:
Isolando temos:
Então gurizada, temos o seguinte:
Resposta
Nossa resposta gurizada, é:
Exercícios de Livros Relacionados
Uma barra circular cheia é feita de um material considerado elastoplástico chamado de T E e ϕ E ⋅ respectivamente,o torque se o ângulo de torção no início do escoamento, determine o ângulo de torção f
O eixo A B é feito de um material elastoplástico com T E =90M P a e G = 30G P a .Para o carregamento mostrado , determine (a) o raio do núcleo elástico da seção transversal do eixo e (b) o ângulo de t
Um eixo de seção vazada tem 0,9 m de comprimento e a seção transversal mostrada. O aço é considerado elastoplástico com τ E = 180M P a e G = 77,2 G P a . Determine a o ângulo de torção quando a seção
Um eixo de seção vazada tem 0,9 m de comprimento e a seção transversal mostrada. O aço é considerado elastoplástico com τ E = 180M P a e G = 77,2 G P a . Determine o torque aplicado e o correspondente
O torque T causa uma rotação de 2° na extremidade B da barra de aço inoxidável mostrada. Sabendo que b = 20m meq u eG = 75G P a , determine a máxima tensão de cisalhamento na barra.