Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 53
O eixo é feito de aço e tem diâmetro de 15 mm. Determine sua deflexão máxima. Os mancais em A e B exercem somente reações verticais sobre o eixo.
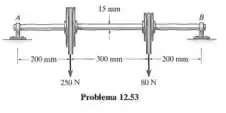
Passo 1
Dados da questão:
A questão pede:
Estratégia de resolução: Vamos calcular equações para a inclinação e a linha elástica. Depois, utilizamos os dados da questão para calcular o produto . Com esses dados podemos determinar o ponto em que a equação da inclinação é igual a zero. Neste ponto a deflexão é máxima.
Passo 2
Começamos pelas reações de apoio:
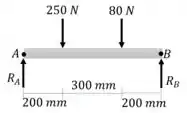
Passo 3
Vamos utilizar a tabela 12.2 para gerar uma equação de descontinuidade para o momento fletor.
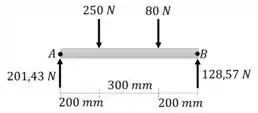
Para simplificar a expressão, podemos ignorar as forçar pontuais que ficam na extremidade final da viga. Tambem podemos dizer que , desde que
Passo 4
Agora vamos integrar a equação do momento para conseguir a equação da inclinação
Obtemos:
Passo 5
Agora vamos integrar a equação da inclinação para obter a equação da linha elástica
Obtemos:
Passo 6
Vamos utilizar as condições de contorno para determinar as constantes.
O ponto A é um rolete. A condição de contorno neste rolete é:
Aplicando na equação da linha elástica
Passo 7
O ponto B também é um rolete. A condição de contorno neste rolete é:
Aplicando na equação da linha elástica
Passo 8
Pronto! Agora temos as equações da inclinação e da linha elástica:
Passo 9
Para obter valores para essas equações precisamos calcular o momento de inércia. A questão nos diz que é um eixo de seção circular de 15 mm de diâmetro. Então o momento de inércia é:
Assim o produto é:
Passo 10
Agora vamos descobrir em que ponto a inclinação é zero.
Vamos aproveitar essa equação para plotar os pontos chaves desse gráfico:
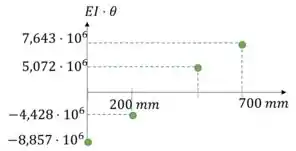
Pelos pontos chaves, sabemos que o gráfico da inclinação atinge o zero em algum ponto entre 200mm e 500mm. Então vamos procurar nessa faixa de valores:
Como estamos trabalhando em uma faixa restrita de valores, o colchete de Macauley pode ser agora tratado como parêntesis.
Agora basta resolver a expressão:
Resolvendo a equação de segundo grau:
O segundo valor está fora da viga, então desconsideramos! Então o ponto de máxima deflexão é:
Passo 11
Vamos finalizar a questão aplicando o valor do ponto máximo na equação da linha elástica:
Então:
Aplicando o valorde