Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 130
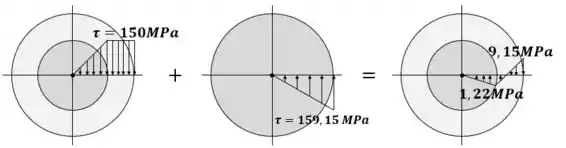
O eixo é feito de um material elástico perfeitamente plástico como mostra a figura. Faça um gráfico da distribuição da tensão de cisalhamento que age ao longo de uma linha radial se o eixo for submetido a um torque T=2 kNm. Qual será a distribuição da tensão residual no eixo quando o torque for removido.
Passo 1
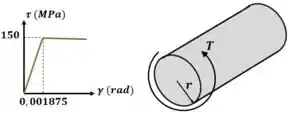
Dados da questão:
A questão pede a distribuição de tensão residual sobre o eixo. Para calcular isso primeiro definimos a distribuição de tensão que gera a torção plástica, e a distribuição de tensão de recuperação elástica.
Estratégia de resolução:
- Calcular o momento de inércia.
- Definir qual o tipo de deformação (elástica ou elástico-plástica ou plástica)
- Desenhar a distribuição de tensão que gera a torção plástica.
- Calcular a tensão de recuperação.
- Desenhar a distribuição de tensão elástica.
- Desenhar a distribuição de tensão residual.
Passo 2
O momento de inércia da seção transversal
Passo 3
Vamos supor que a deformação é elástica. Qual o maior torque que pode atuar?
O torque que a questão nos fornece é maior. Então o regime não é elástico!
Mas qual é o torque mínimo para obter um regime totalmente plástico? Podemos calcular isso com a equação 5.27
O torque plástico também é maior que o torque fornecido na questão. Isso quer dizer que o eixo está em regime elástico-plástico. Então, vamos definir qual é o raio do núcleo elástico com a Equação 5.26
Isolando o raio elástico:
Substituindo os valores:
Passo 4
Para saber o comportamento da tensão na seção transversal, devemos olhar pro gráfico tensão-deformação. Observe que na zona de comportamento elástico a tensão cresce de maneira linear. Já na região plástica a tensão se mantém sempre constante.
O comportamento da tensão na seção transversal é semelhante. No núcleo elástico a tensão cresce até atingir a tensão de escoamento. Na zona plástica a tensão se mantém constante e igual a tensão de escoamento.
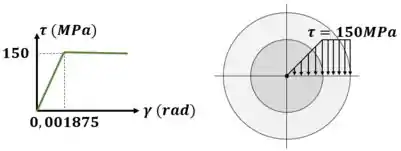
Passo 5
Uma vez que o torque é aliviado, a energia elástica acumulada é liberada “destorcendo” o eixo, gerando uma recuperação em parte da deformação. O torque de destorce o eixo é igual ao torque original, mas em sentido contrário.
O comportamento de “destorção” é elástico, então a tensão máxima que destorce o eixo é calculada pela equação do torque:
É interessante calcular a tensão que atua no limiar do núcleo elástico:
Passo 6
Ao longo da seção transversal, a tensão de recuperação tem comportamento elástico ao longo de toda a seção transversal:
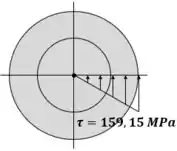
Passo 7
A distribuição de tensão residual é uma soma vetorial das duas distribuições de tensões.
A tensão na extremidade do núcleo elástico é:
A tensão na parte mais exterior do eixo:
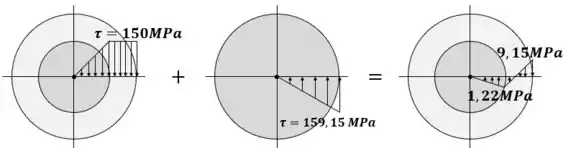
Resposta
