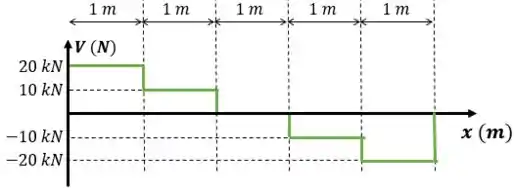
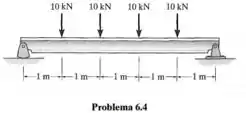
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
Passo 1
Fala aí! Essa questão tem um passo a passo muito comum. Vamos seguir ele que é sucesso!
Começamos desenhando o diagrama de corpo livre.
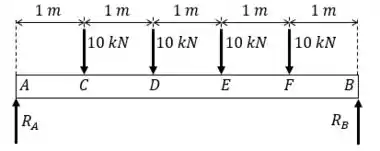
Como o carregamento e as reações são perfeitamente simétricos:
Aplicando as equações de equilíbrio
Como :
Fofo, né? Vamos seguir!
Passo 2
Questões com vários carregamentos pontuais são resolvidas mais rapidamente pelo método gráfico. E aqui eu tenho um bizu para te dar. Vou te apresentar a “Jornada do Cortante”.
Nome bonito, né? O funcionamento é mais ainda. Se liga! A ideia é você ir desenhando o diagrama seguindo o sentido das setas das forças verticais no DCL. E valor que coloca no gráfico é o valor das forças.
Vem ver:
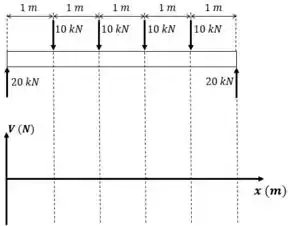
A gente tem ali no começo um vetor que vale para cima. Então o que a gente faz? Vai no nosso diagrama e anda para cima em linha reta, e depois fica constante até o próximo ponto que tenha carga.
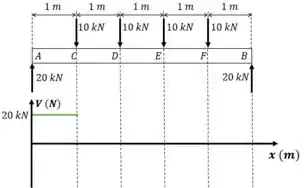
Aí a gente encontra uma força para baixo que vale . Então a gente continua de onde parou e anda para baixo. Mas repara, estávamos em , então andar para baixo, deixa a gente em . Tá bem?
Depois, a gente anda constante até o próximo ponto.
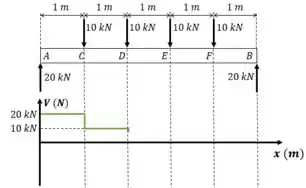
Nesse a gente desce também, porque nossa força vale isso e está virada para baixo. Aí vamos parar em . E continuamos constante até o próximo ponto onde há força.
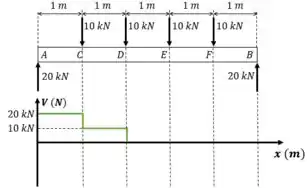
De novo, temos uma força para baixo, aí a gente desce e chega em . Continua constante até .
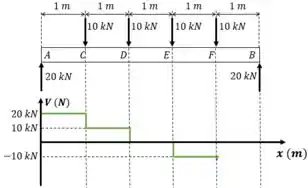
Aí desce de novo:
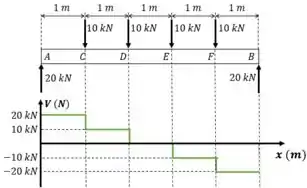
Ponto B: Agora a gente encontra uma força para cima de . Então a gente sobe .
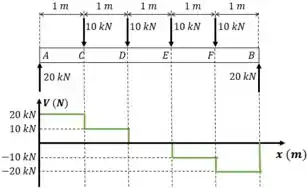
Pronto, o gráfico do cortante está completo. E repara que no final, a gente chegou em zero. Se sua estrutura está em equilíbrio, isso deve acontecer, tá?
Passo 3
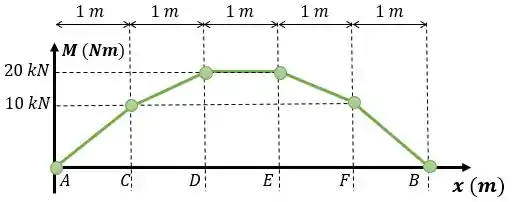
O gráfico de momento fletor é a integral do gráfico de esforço cortante. Então, podemos calcular a intensidade do momento fletor calculando a área abaixo do gráfico de esforço cortante. Então, vamos calcular a área abaixo de todas as seções do gráfico de esforço cortante e depois construir o gráfico de momento fletor.
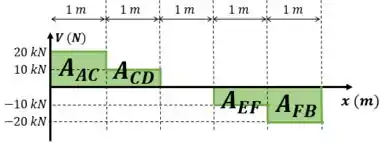
Com o valor das áreas, podemos calcular o momento em cada ponto
Distribuímos os pontos em no plano cartesiano
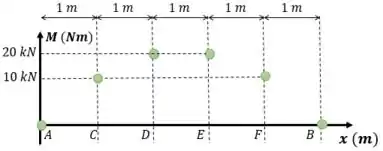
Como as linhas no gráfico de esforço cortante representam constantes, e a integração de constantes são retas inclinadas, vamos ligar os pontos do gráfico com retas:
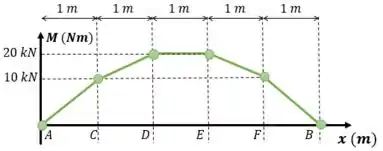
Prontinho!
Resposta