Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 93
O eixo é feito de plástico e tem seção transversal elíptica. Se for submetido ao carregamento de torção mostrado, determine a tensão de cisalhamento no ponto e mostre a tensão de cisalhamento em um elemento de volume localizado nesse ponto. Determine também o ângulo de torção na extremidade . .
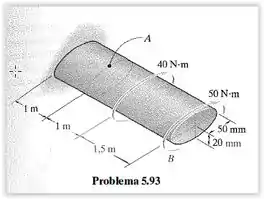
Passo 1
Olá, galerinha! Tudo bem com vocês?
Vamos primeiro verificar o que o problema pede:
- Determinar a tensão de cisalhamento no ponto ;
- Mostrar a tensão de cisalhamento em um elemento de volume localizado nesse ponto;
- Determinar o ângulo de torção na extremidade .
Módulo de elasticidade transversal do plástico: .
Agora é importante desenhar o diagrama de corpo livre e fazer o equilíbrio dos torques.
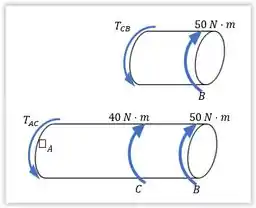
Na seção :
Na seção :
Passo 2
O ponto está localizado na seção , e,
A seção transversal do eixo é uma elipse, então usaremos a fórmula:
Em que é a metade da diagonal maior e é a metade da diagonal menor. Calculando tensão de cisalhamento nesse ponto, temos:
Passo 3
O nosso próximo passo é mostrar a a tensão de cisalhamento em um elemento de volume localizado no ponto .
Mas, como fazemos isso? 
É simples, basta você determinar a localização de uma tensão no elemento de volume. As outras são reações a ela para manter o corpo em equilíbrio.
Essa primeira tensão que determinaremos é uma tensão resultante do torque localizada no centro da face frontal do elemento de volume e orientada para a esquerda, pois o torque é no sentido anti-horário.
Sendo assim, as outras tensões serão reações, a fim de manter o corpo em equilíbrio.
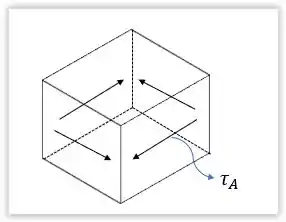
Passo 4
Resta, por fim, determinar o ângulo de torção na extremidade , que corresponde a:
Como se trata de uma elipse a fómula é dada por:
Temos então:
Como o denominador é o mesmo, podemos simplificar e colocar em evidência:
Convertendo para radianos: