Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 46
Resolver o Prob 3.45, considerando que o eixo AB é substituído por um eixo vazado de mesmo diâmetro externo e com de diâmetro interno.
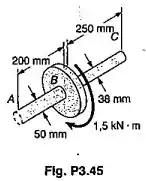
Passo 1
Vamos começar calculando o momento de inércia de cada barra:
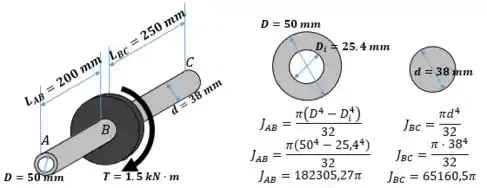
Passo 2
Esta é uma situação estaticamente indeterminada. A questão dá pra gente o valor total do torque, mas não diz a quantidade de torque que é aplicada em cada barra.
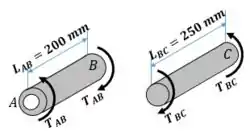
Como esse é um sistema estático, a gente pode afirmar que:
Mas isso ainda não ajuda muito. A gente conhece o valor de , mas e são desconhecidos.
Precisamos de uma segunda equação que relacione e
Se a gente reparar bem, vamos perceber que o disco em B conecta as duas barras. Então, se as duas barras estão conectadas, o ângulo de torção deve ser o mesmo nas duas barras. Podemos usar isso para relacionar os torques!
Primeiro calculamos o ângulo de torção em cada barra:
E igualamos:
A gente pode simplificar o dos dois lados, e depois isolar
Passo 3
Show! Agora é só resolver o sistema:
O resultado será:
Passo 4
Agora a gente calcula a tensão em AB:
Primeiro vamos calcular o valor do raio:
E aplicar a equação da tensão de cisalhamento:
Passo 5
E calcula a tensão em BC pelo mesmo procedimento:
Calculamos o valor do raio:
E aplicamos a equação da tensão de cisalhamento: