Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 55b

Um eixo maciço e um eixo vazado são feitos de mesmo material e têm o mesmo peso e o mesmo comprimento. Expressando por n a reção c 1 / c 2 , mostrar que a relação T m / T v , entre o torque T m do eix maciço e T v do eixo vazado é: (a) 1 - n 2 / ( 1 + n 2 )   se a máxima tensão for a mesma em ambos os eixo. (b) ( 1 - n 2 ) / ( 1 + n 2 )   se o ângulo de torção for o mesmo em ambos os eixos.

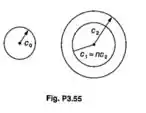
Passo 1

Agora vamos considerar que os ângulos de torção são iguais:

ϕ m = ϕ v

T m L G J m = T v L G J v

Como os material é o mesmo, e o comprimento também é o mesmo, então podemos simplificar G e L

T m J m = T v J v

Vamos isolar T m / T v

T m T v = J m J v

Vamos aplicar as expressões:

T m T v = π 2 c 2 4 1 - n 2 2 π 2 c 2 4 1 - n 4

Simplificamos:

T m T v = 1 - n 2 2 1 - n 4

Para sair dessa vamos novamente usar o produto notável:

1 4 - n 4 ⇒ 1 2 2 - n 2 2 ⇒ 1 2 - n 2 1 2 + n 2

Aplicando:

T m T v = 1 - n 2 2 1 2 - n 2 1 2 + n 2

E simplificamos novamente:

T m T v = 1 2 - n 2 1 2 + n 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

500 N ⋅ m no eixo de alumínio ABCD, quando ele está girando a uma rotação constante. Sabendo que G = 27 GPa e que os torque exercidos sobre as polias B e C são aquelas mostrados na figura, determine o
O eixo cheio AB tem um diâmetro d s = 1.75i n e é feita de aço com G = 11.2 × 10 6 p s i e τ a l l = 12K s i , enquanto a luva CD é feita de latão com G = 5.6 × 10 6 p s i e τ a l l = 7K s i . Determi
O navio em A está começando a perfurar um poço de petróleo no fundo do oceano a uma profundidade de 1524 m. Sabendo que o topo da broca de aço G = 77,2G P a de 203 mm de diâmetro dá duas voltas comple
O eixo cheio AB tem diâmetro d s = 1.5i n , e é feito de aço com G = 11,2X 10 6 psi e τ a l l = 7 psi, enquanto a luva CD é feita de latão com G=5,6 x 10 6 psi e τ a l l = 7 ksi. Determine o maior âng
Três eixos se seção transversal cheia são conectados pelas engrenagens A e B mostradas. Sabendo que G = 77,2 GPa, determine o ângulo de torção entre (a) A e B (b) A e C.