Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 55a

Um eixo maciço e um eixo vazado são feitos de mesmo material e têm o mesmo peso e o mesmo comprimento. Expressando por n a reção c 1 / c 2 , mostrar que a relação T m / T v , entre o torque T m do eix maciço e T v do eixo vazado é: (a) 1 - n 2 / ( 1 + n 2 )   se a máxima tensão for a mesma em ambos os eixo. (b) ( 1 - n 2 ) / ( 1 + n 2 )   se o ângulo de torção for o mesmo em ambos os eixos.

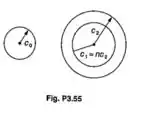
Passo 1

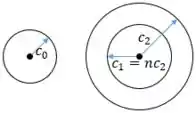
A primeira coisa a se notar é: Se os dois eixos tem o mesmo e o mesmo comprimento, então eles tem que ter a mesma área.

P a r a   o   e i x o   m a c i ç o P a r a   o   e i x o   v a z a d o A = π c 0 2 A = π c 2 2 - c 1 2

Igualando:

π c 0 2 = π c 2 2 - c 1 2

Colocando c 2 em evidência:

π c 0 2 = π c 2 2 ( 1 - n 2 )

E isolamos c 0

c 0 = c 2 2 ( 1 - n 2 )

c 0 = c 2 ( 1 - n 2 )

Passo 2

Vamos aproveitar pra calcular o momento de inércia polar de cada eixo.

Para o eixo maciço:

J m = π 2 c 0 4

J m = π 2 c 2 1 - n 2 4

J m = π 2 c 2 4 1 - n 2 2

Para o eixo vazado:

J v = π 2 ( c 2 4 - c 1 4 )

J v = π 2 c 2 4 1 - n 4

Passo 3

Se a tensão é a mesma para os dois eixos, então:

τ m = τ v

T m ⋅ c 0 J m = T v ⋅ c 2 J v  

Vamos isolar T m / T v

T m T v = J m ⋅ c 2 c 0 ⋅ J v

Vamos aplicar as expressões:

T m T v = π 2 c 2 4 1 - n 2 2 ⋅ c 2 c 2 ( 1 - n 2 ) ⋅ π 2 c 2 4 1 - n 4

T m T v = 1 - n 2 2 ( 1 - n 2 ) ⋅ 1 - n 4

Beleza e como a gente sai dessa agora? Basta lembrar dos produtos notáveis.

a 2 - b 2 = ( a - b ) ( a + b )

Baseado nisso podemos fazer:

1 4 - n 4 ⇒ 1 2 2 - n 2 2 ⇒ 1 2 - n 2 1 2 + n 2

Vamos aplicar no denominador:

T m T v = 1 - n 2 2 ( 1 - n 2 ) ⋅ 1 2 - n 2 1 2 + n 2

E agora vamos simplificar

T m T v = 1 2 - n 2 ( 1 - n 2 ) ⋅ 1 2 + n 2

E simplificando mais uma vez chegamos nos resultados:

T m T v = ( 1 - n 2 ) 1 2 + n 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As hélices de um navio estão acopladas a um eixo maciço de aço A-36 com 60 m de comprimento, diâmetro externo de 340 mm e diâmetro interno de 260 mm. Se a potência de saída for 4,5 MW quando o eixo gi
O eixo de transmissão tubular para a hélice de um aerodeslizador tem 6 m de comprimento. Se o motor transmitir 4 MW de potência ao eixo quando as hélices giram a 25 rad/s, determine o diâmetro interno
O eixo de aço A-36 é composto pelos tubos A B e C D e uma seção maciça B C . Está apoiado em mancais lisos que permitem que ele gire livremente. Se as engrenagens, presas às extremidades do eixo, fore
As extremidades estriadas e engrenagens acopladas ao eixo de aço A-36 estão sujeitas aos torques mostrados. Determine o ângulo de torção da engrenagem C em relação à engrenagem D . O eixo tem diâmetro
A turbina desenvolve 150k W de potência, que é transmitida às engrenagens de tal modo que C e D recebem quantidades iguais. Se a rotação do eixo de aço A-36 de 100m m de diâmetro for ω=500r e v / m i