Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 35

500   N ⋅ m no eixo de alumínio ABCD, quando ele está girando a uma rotação constante. Sabendo que G = 27 GPa e que os torque exercidos sobre as polias B e C são aquelas mostrados na figura, determine o ângulo de rotação entre:

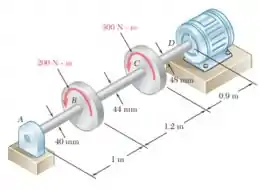
(a) B e C

(b) B e D.

Passo 1

Bora lá, vamos ver o Ângulo de torção entre B e C.

T B C = 200   N / m , L B C = 1.2   m

c = 1 2 d = 0.022   m , G = 27 × 10 9 P a

J B C = π 2 c 4 = 367.97 × 10 - 9 m

ϕ B C = T L G J = 200 1.2 27 × 10 9 367.97 × 10 9 = 24.157 × 10 - 3 r a d

ϕ B C = 1.384 °

Passo 2

Podemos prosseguir para o eixo BD!

  T CD =500 N/m , L CD =0.9 m ,

c= 1 2 d=0.024 m , G=27× 10 9 Pa

  J CD = π 2 c 4 = π 2 0.024 4 =521.153× 10 -9 m 4

  ϕ CD = 500 0.9 27× 10 9 521.153× 10 9 = 31.980 -3 rad

ϕ B D = ϕ B C + ϕ C D = 24.157 × 10 - 3 + 31.980 × 10 - 3 = 56.137 × 10 - 3 r a d

ϕ BD = 3.22 °

Resposta

  1. B C = 1.384 °
  2. BD = 3.22 ° .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo de raio c é submetido a um torque distribuído t , medido como torque/comprimento do eixo. Determine as reações nos apoios A e B.
Determine a rotação da engrenagem em E no Problema 5.81.
O eixo cônico está confinado pelos apoios fixos em A e B . Se for aplicado um torque T em seu ponto médio, determine as reações nos apoios.
Determine a rotação da junta B e a tensão de cisalhamento máxima absoluta no eixo do Problema 5.85 .
O eixo de aço tem 300m m de comprimento e é parafusado em uma parede com uma chave de torque. Determine as maiores forças conjugadas F que podem ser aplicadas ao eixo sem provocar o escoamento do aço.