Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 94
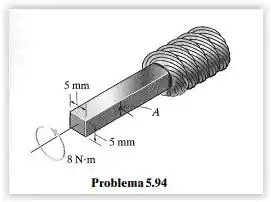
O eixo quadrado é usado na extremidade de um cabo de acionamento para registrar a rotação do cabo em um medidor. Se tiver as dimensões mostradas na figura e for submetido a um torque de , determine a tensão de cisalhamento no eixo no ponto . Faça um rascunho da tensão de cisalhamento sobre um elemento de volume localizada nesse ponto.
Passo 1
Olá pessoal, tudo bem?
O problema pede que determinemos a tensão de cisalhamento no ponto e a também um rascunho da tensão sobre um elemento de volume localizada nesse ponto. Nos fornece como dados:
Primeiro iremos determinar a tensão no ponto .
Como a seção transversal do eixo é quadrada, a fórmula para a tensão máxima de cisalhamento é:
Substituindo os valores que foram dados pela questão:
Passo 2
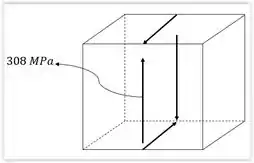
Agora iremos para o segundo passo, um rascunho da tensão de cisalhamento sobre um elemento de volume localizado em .
Mas, como fazemos isso? 
É simples, basta você determinar a localização de uma tensão no elemento de volume. As outras são reações a ela para manter o corpo em equilíbrio.
Essa primeira tensão que determinaremos é uma tensão resultante do torque localizada no centro da face frontal do elemento de volume e orientada para cima, pois o torque é no sentido anti-horário. (Observe que o ponto está na lateral do eixo).
Sendo assim, as outras tensões serão reações, a fim de manter o corpo em equilíbrio.
