Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 102
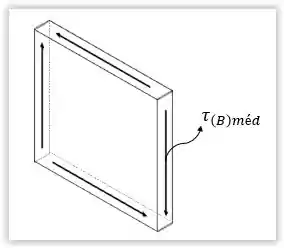
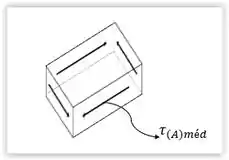
Um tubo com as dimensões mostradas na figura é submetido a um torque a . Desprezando as concentrações de tensão em seus cantos, determine a tensão de cisalhamento média no tubo nos pontos e . Mostre a tensão de cisalhamento nos elementos de volume localizados nesses pontos.
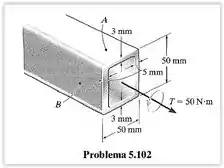
Passo 1
Olá, pessoal! Ânimo, que já, já essa questão está no papo!
O enunciado pede que determinemos a tensão de cisalhamento média no tubo em dois pontos, e , e que mostremos ela nos elementos de volume localizados nesses pontos. O tubo é submetido a um torque de .
A fómula da tensão de cisalhamento média é dada por:
Vamos logo calcular a área média contida no contorno da linha central da espessura do tubo, .
A ilustração nos fornece as medidas das laterais, que são iguais por se tratar de uma seção quadrada, e a espessura da face onde está o ponto e da face onde está o ponto . Para melhor compreender, vamos observar a figura abaixo:
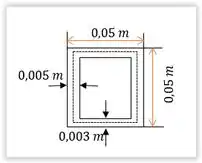
A linha pontilhada no desenho é o contorno da área média.
A área média será dada por:
Onde é a base desse contorno e é a altura do contorno.
Para calcular vamos primeiro encontrar as medidas de cada lado. (considerando que lados paralelos tem a mesma expessura)
A área média é igual a:
Passo 2
Agora vamos calcular a tensão média de cisalhamento em cada ponto. Lembrando que o ponto está na superfície superior, onde a espessura é e o ponto está na lateral, onde a espessura é .
Ponto :
No ponto :
Passo 3
O próximo passo é a mostrar a tensão de cisalhamento em um elemento de volume localizado nos pontos e .
Mas, como fazemos isso? 
É simples, basta você determinar a localização de uma tensão no elemento de volume. As outras são reações a ela para manter o corpo em equilíbrio.
Tensão de cisalhamento no elemento de volume no ponto , que se encontra na parte superior do tubo:
A primeira tensão que determinaremos é uma tensão resultante do torque localizada no centro da face frontal do elemento de volume e orientada para a esqueda, no sentido que o torque tem quando passa pelo ponto , pois o torque é no sentido anti-horário. Assim:
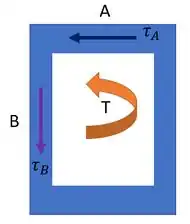
As outras tensões serão reações, a fim de manter o corpo em equilíbrio.
Tensão de cisalhamento no elemento de volume no ponto , situado na lateral do tubo:
A primeira tensão que determinaremos é uma tensão resultante do torque localizada no centro na face frontal do elemento de volume e orientada para baixo, também no sentido do torque quando passa por , devido ao torque estar no sentido anti-horário.
As outras tensões serão reações, a fim de manter o corpo em equilíbrio.
