Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 156

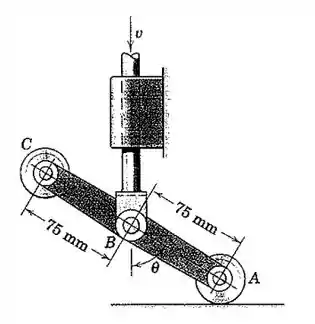
Os componentes do dispositivo de comutação do prob. 5/85 são mostrados novamente aqui. Se a velocidade v da haste de controle é de 0,9 m/s e está diminuindo na taxa de 6 m/s² quando θ = 60 ° , determine o módulo da aceleração de C.

Passo 1

Galera, primeiro vamos organizar todos os dados do enunciado e fazer um esboço do que realmente importa no mecanismo.

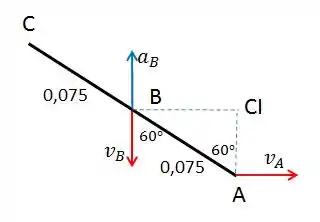
Vamos começar calculando a velocidade angular da barra. Isso pode ser feito pelo método do Centro Instantâneo, como pode ser visto pela figura.

ω = v B r B / C I = - 0 , 9 - 0 , 075 s e n 60 = 13,856 k ^   r a d / s

Com isso, podemos calcular o módulo da velocidade de A em relação a B.

v A / B = ω × r A B = 1,04   m / s

Passo 2

Neste passo, vamos usar a equação da aceleração relativa para os pontos A e B.

a B = a A + a B / A n + a B / A t

Onde:

a B / A n = ω × ω × r B / A = - 13,856 2 - 0,075 s e n 60 i ^ + 0 , 075 c o s 60 j ^ = 12,47 i ^ - 7,2 j ^ m / s 2

a B / A t = α × r B / A = α - 0,0375 i ^ - 0,065 j ^ m / s 2

A aceleração de A está na direção horizontal do seu curso.

Agora, vamos substituir os valores encontrados na equação da aceleração relativa:

6 j ^ = a A i ^ + 1 2,47 i ^ + 7,2 j ^ + α - 0,0375 i ^ - 0,065 j ^

Decompondo nas direções, temos o sistema:

0 = a A i ^ + 2,47 i ^ + α - 0,0375 i ^

6 j ^ = - 7,2 j ^ + α - 0,065 j ^

Resolvendo o sistema, temos:

α = - 203 k ^   r a d / s 2

a A = - 20,08 i ^   m / s 2

Passo 3

Agora, vamos repetir o passo anterior, mas fazendo a aceleração relativa de C e B.

a C = a B + a C / B n + a C / B t

Onde:

a C / B n = ω × ω × r C / A = ω × ω × r C / B = - 13,856 2 - 0,075 s e n 60 i ^ + 0,075 c o s 60 j ^ = 12,47 i ^ - 7,2 j ^ m / s 2

a C / B t = α × r C / B = α - 0,0375 i ^ - 0,065 j ^ m / s 2

Agora, vamos substituir os valores encontrados na equação da aceleração relativa:

a C = 6 j ^ + 12,47 i ^ - 7,2 j ^ + α - 0,0375 i ^ - 0,065 j ^

Decompondo nas direções, temos o sistema:

a C i ^ = 1 2,47 i ^ - 203 - 0,0375 i ^

a C j ^ = 6 j ^ - 7,2 j ^ - 203 - 0,065 j ^

Resolvendo o sistema, temos:

a C i ^ = 20,08   i ^   m / s 2

a C j ^ = 11,2 j ^   m / s 2

Como é pedido o módulo da aceleração de C:

a C = 20,08 2 + 11,2 2 = 23,4   m / s 2

Resposta

a C = 23,4   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As duas hélices com 800 mm de raio giram no sentido anti-horário com uma velocidade angular constante ω = θ ˙ = 2r a d / s em torno do eixo em O montado em um bloco deslizante. A aceleração do bloco é
Com referencia às hélices e o bloco deslizante do mancal do Prob. 5/123 onde a O = 3 m / s 2 . Se θ ¨ = 5 r a d / s 2 e θ ˙ = 0 quandoθ = 0 , encontre a aceleração do ponto A para esse instante.
15.220. A barra AB está soldada em uma placa de 300 mm de raio que gira com uma taxa constante 1 6 rad /s. Sabendo que o colar D se desloca na direção da extremidade B da barra a uma velocidade consta
15.221. A barra dobrada mostrada na figura gira à taxa constante 1 3 rad /s. Sabendo que o colar C se desloca na direção do ponto D com uma velocidade relativa constante u 1 m/s, determine, para a pos
16.109. O disco está se deslocando para a esquerda de tal maneira que ele tem uma aceleração angular α = 8 r a d / s 2 e velocidade angular ω = 3 r a d / s no instante mostrado. Se ele não desliza em