Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 90
No eixo de seção variável mostrado na figura, que tem um adoçamento de um quarto de circunferência completa, a tensão de cisalhamento admissível é de MPa. Sabendo que , determine o maior torque admissível que pode ser aplicado ao eixo se (a) e (b) .
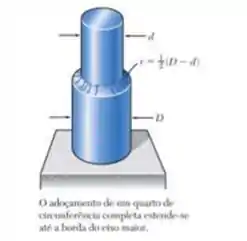
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine o maior torque admissível que pode ser aplicado ao eixo. Comecemos trazendo alguns dados e conversões:
Primeiro, vamos ver os dados:
O raio e a relação diâmetro e raio é dado a seguir:
Onde e o diâmetro , agora podemos determinar o torque a partir da equação de cisalhamento.
Passo 2
De maneira similar ao passo 1 vamos determinar a torção a partir dos dados abaixo :D
Sabendo que e temos:
Resposta
(a)
(b) .
Exercícios de Livros Relacionados
A curva mostrada na F i g .P 3.89 e F i g .P 3.92 pode ser aproximada pela relação: τ = 27,8x10 9γ - 1,390x10 12γ 2 Usando esta relação e as equações (3.2) e (3.26) resolver o problema indicado.
O eixo maciço mostrado é feito de um aço doce, que é considerado ser elastoplástico com G = 77G P a e τ e = 145M P a . Sabendo-se que um torque T é aumentado até que o raio do núcleo elástico atinja 6
No Prob. 3.95, determinar o ângulo de torção permanente (residual) no eixo.
No Prob. 3.98, determinar o ângulo de torção permanente no eixo.
O eixo vazado mostrado é feito e um aço doce, que é considerado ser elastoplástico com G = 77G P a e τ e = 145M P a . A intensidade T do torque é lentamente aumentando, até que a zona plástica atinja