Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 92
O eixo circular de seção cheia mostrado na figura é feito de um aço considerado elastoplástico com . Determine a intensidade do torque aplicado quando a zona plástica tem (a) de profundidade e (b) de profundidade.
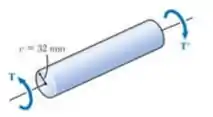
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a intensidade do torque aplicado quando a zona plástica tem (a) de profundidade e (b) de profundidade.
Então primeiramente vamos começar trazendo os dados :
Agora temos que determinar o torque, vem comigo :D
Considerando que:
Substituindo os valores temos:
Passo 2
E por último, vamos calcular para a alternativa (b), considerando os seguintes dados:
Substituindo os valores temos:
Resposta
(a)
(b) .
Exercícios de Livros Relacionados
O tubo de bronze C 86100 tem diâmetro externo de 37,5m m e espessura de 3m m . A conexão em C está sendo apertada com uma chave de torque. Se for aplicada uma força F=100N , determine a tensão de cisa
O eixo é feito de aço-ferramenta L2, tem diâmetro de 40m m e está preso em suas extremidades A e B . Se for submetido ao conjugado, determine a tensão de cisalhamento máxima nas regiões A C e C B .
O eixo é composto por uma seção maciça de aço A B e uma porção tubular feita de aço com núcleo de latão. Se o eixo estiver preso a um apoio rígido A e for aplicado um torque T =50N ⋅ m a ele em C , de
O eixo de aço é composto por dois segmentos: AC, com diâmetro de 12 mm e CB, com diâmetro de 25 mm. Se estiver preso em suas extremidades A e B e for submetido a um torque de 750 N . m , determine a t
O eixo de aço A-36 tem diâmetro de 50m m e está sujeito aos carregamentos distribuídos e concentrados mostrados. Determine a tensão de cisalhamento máxima absoluta no eixo e construa um gráfico para o