Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 107

Um eixo de seção vazada tem 0,9 m de comprimento e a seção transversal mostrada. O aço é considerado elastoplástico com τ E = 180   M P a e G = 77,2     G P a . Determine o torque aplicado e o correspondente ângulo de torção a no limiar do escoamento e b quando a zona plástica atinge 10   m m de profundidade.

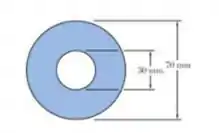
Passo 1

E ai gurizada tudo belezinha? Espero que sim!! O enunciado pede que a gente determine o torque aplicado e o correspondente ângulo de torção no limiar do escoamento e quando a zona plástica atinge 10   m m de profundidade. Então vamos, notem abaixo as medias do nosso eixo, e partiu calcular !!!

a No início do escoamento, a distribuição de tensão é a distribuição elástica e podemos considerar a seguinte relação da tensão de cisalhamento

τ m a x = τ y

Os raios podem interno e externo podem ser obtidos assim:

c 2 = 1 2 d 2 = 0,035 m , c 1 = 1 2 d 1 = 0,015 m

Agora podemos determinar J para então chegarmos na tensão de cisalhamento , vem comigo, só aplicação de fórmula :D

J = π 2 c 2 4 - c 1 4 = π 2 0,035 4 - 0,015 4 = 2,2777   x 10 - 6 m

A tensão de cisalhamento é dada por:

τ m a x = τ y = T y c 2 J = T y = J τ y c 2 = 2,2777   x   10 - 6 180   x     10 6 0,035 = 11,7139   x   10 3   N ⋅ m

T y = 11,71   k N ⋅ m

Agora sim gurizada podemos determinar o ângulo torção

φ y = T y L G J = 11,7139   x   10 3 0 , 9 77,2   x   10 9 2,2777   x   10 - 6 = 59,956   x   10 - 3   r a d

φ y = 3,44 °

Passo 2

Na questão B ele pede para que a gente encontre o torque quando a zona plástica atinge 10   m m de profundidade, então temos que considerar essa profundidade subtraindo do diâmetro fornecido pelo exercício...

p y = c 2 - ι = 0,035 - 0,010 = 0,025   m

E o ângulo podemos determinar aplicando na equação a seguir:

φ = T y L G J = 11,7139   x   10 3 0,9 77,2   x   10 9 0,025 = 59,956   x   10 - 3   r a d

φ y = 4,81 °

E o torque pode ser determinado da seguinte maneira, primeiro devemos achar J para daí sim aplica na equação, falta pouco 0/

J 1 = π 2 p y 4 - c 1 4 = π 2 0,025 4 - 0,015 4 = 534,07   x   10 - 9   m 4

Agora podemos encontrar o primeiro torque :D

T 1 = J 1 τ y p y = 534,07   x   10 - 9 180   x   10 6 0,025 = 3,8453   x   10 3   N ⋅ m

Torque T 2 realizado pela zona plástica é dado pela integral abaixo:

T 2 = 2 π ∫ p y c 2   τ y   p 2   d p = 2 π τ y p 3 3 ∫ p y c 2 = 2 π 3 τ y c 2 3 - p y 3

= 2 π 3 180   x   10 6 0,035 3 - 0,025 3 = 10,2730   x   10 3   N ⋅ m

Torque total então é a soma dos torques, barbadinha né :D

T = T 1 + T 2 = 3,8453   x   10 3 + 10,2730   x   10 3 = 14,1183   x   10 3   N ⋅ m = 14,12   k N ⋅ m

Resposta

  1. T y = 11,71   k N ⋅ m e φ y = 3,44 °
  2. 14,12   k N ⋅ m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o eixo de seção circular do Problema 3.98, determine (a) a intensidade do torque T necessário para que eixo sofra um giro de 15 ° e (b) o raio do correspondente núcleo elástico.
A barra circular de seção cheia AB é feita de aço elastiplástico com T E = 151,7M P aeG = 77,2G P a . Sabendo que um torque T = 8473k N * m m é aplicado à barra e depois removido, determine a tensão d
Um eixo sólido de seção circular com 18m m de diâmetro é feito de um material considerado elastoplástico com t y =145M P a e G = 77,2G P a . Para um eixo com 1,2 m de comprimento, determine a máxima t
Uma barra circular cheia é feita de um material considerado elastoplástico chamado de T E e ϕ E ⋅ respectivamente,o torque se o ângulo de torção no início do escoamento, determine o ângulo de torção f
O eixo A B é feito de um material elastoplástico com T E =90M P a e G = 30G P a .Para o carregamento mostrado , determine (a) o raio do núcleo elástico da seção transversal do eixo e (b) o ângulo de t