Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 31

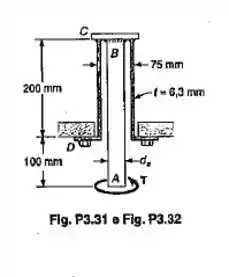
A barra cilíndrica A B tem um diâmetro d s = 38   m m e é feita de um aço com G = 77   G P a   e   τ a d m = 83   M P a ,   enquanto que o tubo C D é feito de um latão com G = 39   G P a e τ a d m = 48,5   M P a . Determinar o maior ângulo de torção permissível na extremidade A.

Passo 1

Primeiramente vamos observar o que temos para a barra AB

d = 38   m m

G = 77   G P a

τ a d m = 83   M P a

ϕ = 0,375 ° = 6,545 × 10 - 3

Para o tubo

G = 39   G P a

τ a d m = 48,5   M P a

Vamos começar então calculando os momentos de inercia do tubo e da barra, tranquilo?

J A B = π 2 19 × 10 - 3 4 = 2,05 × 10 - 7   m 4

Para o tubo

J C D = π 2 37,5 × 10 - 3 4 - 31,2 × 10 - 3 4 = 1,618 × 10 - 6   m 4

Onde 31,2 é o diâmetro todo do tubo (75) dividida por dois, menos a espessura do mesmo.

75 2 - 6,3 = 31,2   m m

Passo 2

O ângulo de torção permissível será aquele quanto tivermos o maior torque possível sem romper o tubo ou a barra. O torque máximo que a barra suporta é de:

T = τ a d m b a r r a J A B ρ A B = 83 × 10 6 × 2,05 × 10 - 7 19 × 10 - 3 = 0,895   k N m

Para a torção admissível do tubo CD:

T = τ a d m t u b o J C D ρ C D = 48,5 × 10 6 × 1,618 × 10 - 7 37,5 × 10 - 3 = 2,093   k N m

Passo 3

Com isso notamos que o maior torque que poderá ser aplicada é 0,895   k N m , pois, caso seja superior a isso, a barra AB não resiste. Então temos que o ângulo será de:

ϕ = 895 × 300 × 10 - 3 2,05 × 10 - 7 × 77 × 10 9

ϕ = 0,017   r a d = 0,98 °

Resposta

ϕ = 0,98 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo de aço A-36 tem diâmetro de 50m m e está preso nas extremidades A e B . Se for submetido ao momento, determine a tensão de cisalhamento máxima nas regiões A C e C B do eixo.
O tubo de bronze C 86100 tem diâmetro externo de 37,5m m e espessura de 0,3m m . A conexão C está sendo apertada com uma chave de torque. Se o torque desenvolvido em A for 16N . m , determine o valorF
O contorno da superfície do eixo é definido pela equação y = e a x , onde a é uma constante. Se o eixo for submetido a um torque T em suas extremidades, determine o ângulo de torção na extremidade A e
Uma mola cilíndrica é composta por um anel de borracha preso a um anel e eixo rígidos. Se o anel for mantido fixo e um torque T for aplicado ao eixo rígido, determine o ângulo de torção do eixo. O mód
O eixo composto tem uma seção média que indica o eixo maciço de 20m m de diâmetro e um tubo soldado a flanges rígidas em A e B . Despreze a espessura das flanges e determine o ângulo de torção da extr