Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 33
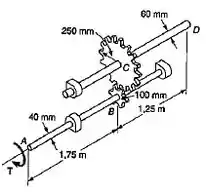
Dois eixos maciços de aço (G=77 GPa) são conectados pelas engrenagens mostradas. Determinar o ângulo de torção da extremidade A, quando nesse ponto um T de 600 N.m é aplicado.
Passo 1
Calculando inicialmente os torques. Vamos analizar as interações entre as engrenagens B e C.
Temos do enunciado que
Passo 2
Vamos fazer aí o passo a passo desse movimento. Primeiramente, girando CD
Calculando o momento de inércia
O ângulo de rotação em CD por conta desse torque será de
Passo 3
Temos a relação entre os raios e o ângulo de rotação da engrenagens como sendo
Passo 4
Agora vamos analizar o intervalo AB
Calculando o momento de inércia
O ângulo de rotação em CD por conta desse torque será de
Passo 5
Pra concluir vamos ter então que o ângulo de rotação em A será
Resposta
Exercícios de Livros Relacionados
Resolva o Problema 5.68 se o torque distribuído for t = ( k x 2 / 3 ) N . m / m .
O parafuso de aço A-36 é apertado dentro de um furo de modo que o torque de reação na haste A B pode ser expresso pela equaçãot=( k x ² )N . m / m ² , onde x é dado em metros. Se um torque T=50N . m f
O tubo de bronze C 86100 tem diâmetro externo de 37,5m m e espessura de 3m m . A conexão em C está sendo apertada com uma chave de torque. Se for aplicada uma força F=100N , determine a tensão de cisa
O eixo é feito de aço-ferramenta L2, tem diâmetro de 40m m e está preso em suas extremidades A e B . Se for submetido ao conjugado, determine a tensão de cisalhamento máxima nas regiões A C e C B .
O eixo é composto por uma seção maciça de aço A B e uma porção tubular feita de aço com núcleo de latão. Se o eixo estiver preso a um apoio rígido A e for aplicado um torque T =50N ⋅ m a ele em C , de