Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 55
O elemento consiste em dois canais U de plástico com 12 mm de espessura colados em A e B. Se a carga distribuída tiver intensidade máxima , determine a tensão de cisalhamento máxima a qual a cola resiste
Passo 1
Dados da questão:
A questão pede a tensão de cisalhamento na cola:
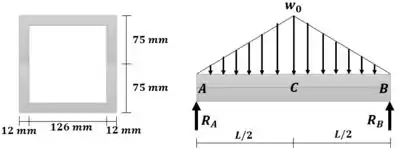
Estratégia de resolução: Primeiro vamos calcular as reações de apoio, e determinar o ponto onde o esforço interno é máximo.
Depois calculamos o momento de inércia e o momento estático da região de interesse. Como a seção é perfeitamente simétrica, não é preciso calcular o centroide.
Por fim, usamos a equação de tensão de cisalhamento para calcular a tensão máxima sobre a cola.
Passo 2
Como o carregamento é perfeitamente simétrico, sabemos que:
Aplicando a equação de equilíbrio:
Passo 3
Agora calculamos o gráfico de esforço cortante utilizando o método gráfico
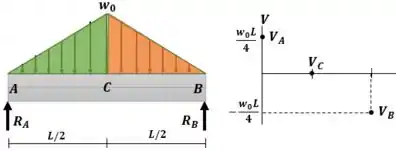
O gráfico resultante é:
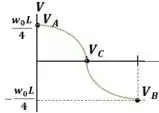
A maior força interna ocorre no ponto A
Passo 4
Agora vamos calcular o momento de inércia da figura. Para isso basta calcular como se a estrutura fosse maciça e depois subtrair o valor da região vazada:
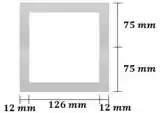
Passo 5
Agora vamos calcular o momento estático de uma região que tenha contato com a cola. A região escolhida está em destaque abaixo:
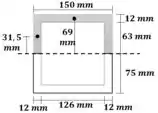
Passo 6
A tensão na região da cola é:
O número “2” aparece na equação acima, pois existem duas regiões de espessura “t” em contato com a cola.
Substituindo o
Substituindo os valores: