Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 92
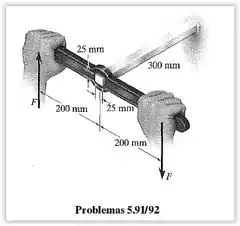
O eixo de aço tem de comprimento e é parafusado em uma parede com uma chave de torque. Determine a máxima tensão de cisalhamento no eixo e o deslocamento que cada força conjugada sofre se o valor das forças conjugadas for .
Passo 1
Oi, pessoal! Tudo bem com vocês?
Então, o problema pede que determinemos a máxima tensão de cisalhamento no eixo e o deslocamento que cada força conjugada sofre se o valor das forças conjugadas forem . Nos fornece como dados:
O primeiro passo é calcular o torque aplicado ao eixo pela chave de torque.
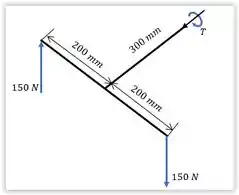
Observando a figura, notamos que ele age no sentindo horário. Pelo diagrama de corpo livre, temos:
Passo 2
Agora vamos calcular a tensão de cisalhamento máxima usando a fórmula para quando a seção transversal do eixo é quadrada:
Em que é a aresta do quadrado e corresponde a , ou seja, . Substituindo, temos:
Passo 3
Precisamos calcular o ângulo de torção para posteriormente encontrarmos o deslocamento das forças. Usamos então a fórmula para eixos com seção transversal quadrada:
OBS: Na tabela do Hibeller essa fórmula está com um erro, falta multiplicar por .
Substituindo os valores, temos:
Passo 4
Agora só falta o deslocamento!
Ele é dado pela distância da aplicação da força até o eixo multiplicado pelo ângulo de torção: