Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 44
O eixo está apoiado sobre mancais que não oferecem resistência a carga axial. Se a tensão normal admissível para o eixo for , determine, com aproximação de , o menor diâmetro do eixo que suportará a carga. Use a teoria de falha da energia de distorção máxima.
Passo 1
Fala aí galera, tudo beeem?. A gente quer achar o diâmetro para essa barra usando a teoria de falha da energia de distorção máxima.
Como a gente tem um eixo com engrenagens, precisamos começar fazendo o diagrama de momento e torque para esse carregamento. Vamos seguir um passo a passo. Vai dar bom!
Vamos então calcular as reações e apoio. O próprio enunciado diz que os mancais só exercem força em e (eles não tem resistência normal, ou seja, na direção ), então temos reações nessas duas direções em e . Vamos considerar todas nos sentidos positivos de e .
Esse é o nosso DCL
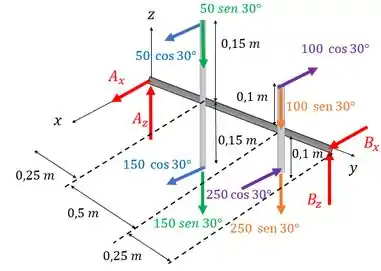
A gente colocou essa barra mais clara para representar o ponto de aplica das forças que estão nos discos, tá?
Aí usando as equações de equiíbrio de forças e momentos, achamos que
Passo 2
Com as reações dos apoios calculadas, vamos esboçar os diagramas de momento fletor para , e :
Para fazer os de momento, a gente calcula os mometos nas seções de aplicação de forças e depois liga os pontos do gráfico por retas, já que só temos cargas concentradas.
Para fazer o de torção, a gente acha o valor para torção nas seções entre as cargas concentradas. Esses valores serão constantes para cada uma dessas seções.
Com esses diagramas a gente escolhe o ponto onde temos a maior combinação de momentos e torque.
Vê que no ponto , temos momentos máximos em relação ao dois eixos e torque máximo. Então a gente escolhe ele. Nesse ponto:
Passo 3
Agora, precisamos encontrar o raio do eixo, para depois calcularmos o diâmetro. Mas precisamos achar uma expressão para pela teoria de falha da energia de distorção máxima. Ela diz que:
Pela transformação de tensões, temos essa expressão para as tensões principais e :
Na nossa seção só temos tensão normal em já que os momentos em e causam tensão normal nessa direção na nossa seção. Ela é dada pela fórmulinha do momento . E a tensão de cisalhemento pela fórmulinha da torção . Ficamos com algo assim:
Onde e . Substituindo ali em cima e simplificando
Passo 4
Subsituindo essas tensões principais na expressão da teoria:
Usando produtos notáveis:
Abrindo os produtos notáveis e simplificando:
Isolando :
Ufa! Essa vai ser nossa expressão para o raio para essa teoria. Vamos seguir.
Passo 5
Substitiundo os valores:
Logo o diâmetro fica