Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 33

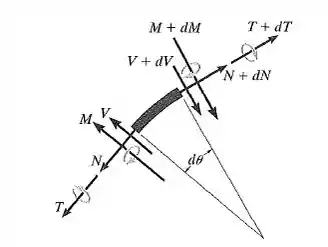
Um elemento diferencial tomado de uma barra curva é mostrado na figura. Mostre que d n d θ = V ; d V d θ = N ; d M d θ =   - T   e d T d θ = M .

dM/dθ

Passo 1

Bom, o primeiro passo desse tipo de questão é montar o diagrama de corpo livre para que possamos vizualisar melhor a situação.

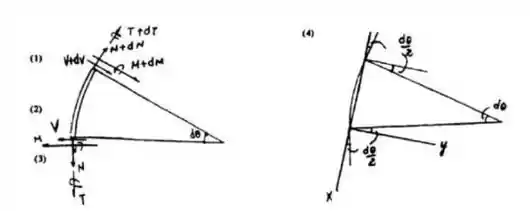
Agora, basta fazer o somatório de forças nas direções.

∑ F x = 0 → N c o s d θ 2 +   V s e n d θ 2 -   N + d N cos ⁡ d θ 2 +   V + d V s e n d θ 2 = 0

∑ F y = 0 → N s e n d θ 2 - V c o s d θ 2 + N + d N s e n d θ 2 +   V + d V cos ⁡ d θ 2 = 0

∑ M x = 0 → T c o s d θ 2 +   M s e n d θ 2 -   T + d T c o s ( d θ 2 ) + M + d M s e n d θ 2 = 0

∑ M y = 0 → T s e n d θ 2 -   M c o s d θ 2 +   T + d T s e n d θ 2 + M + d M cos ⁡ d θ 2 = 0

Como o elemento é infinitesimal, cabem algumas simplificações:

s e n d θ 2 = d θ 2 ; cos ⁡ d θ 2 = 1

O seno de ângulos pequenos tende ao próprio ângulo e o cosseno de ângulos pequenos tende a 1.

Passo 2

Agora basta substituir as simplificações nas equações acima, e ficaremos com:

V d θ - d N + d V d θ 2 = 0

N d θ + d V + d N d θ 2 = 0

M d θ - d T + d M d θ 2 = 0

T d θ + d M + d T d θ 2 = 0

Repare que a última parcela das equações são desprezíveis em vista das demais, logo:

V d θ - d N = 0 → d N d θ = V

N d θ + d V = 0 → d V d θ = - N

M d θ - d T = 0 → d T d θ = M

T d θ + d M = 0 → d M d θ = - T

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as cargas internas resultantes nas seções transversais que passam pelos pontos K e J no guindaste de tambores no Problema 1. 21.
O guindaste de tambores suspende o tambor de 2,5k N . O pino de ligação está conectado à chapa em A e B . A ação de aperto sobre a borda do tambor é tal que somente forças horizontais e verticais são
Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto D no Problema 1. 18.
A viga suporta a carga distribuída mostrada. Determine as cargas internas resultallles que agem na seção transversal que passa pelo ponto C . Considere que as reações nos apoios A e B sejam verticais.
A estrutura do poste de energia elétrica suporta os três cabos, e cada um deles exerce uma força de 4k N nas escoras. Se as escoras estiverem acopladas por pinos em A , B e C , determine as cargas int