Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 34

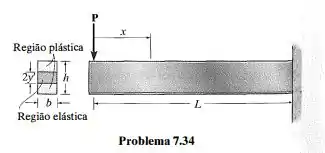
A viga tem seção transversal retangular e está sujeita a uma carga P cuja intensidade é suficiente para desenvolver um momento totalmente plástico M P = P L no apoio fixo. Se o material for elástico-plástico, então, a uma distância x < L , o momento M = P x cria uma região de escoamento, plástico com um núcleo elástico associado a uma altura 2 y ’ . Essa situação foi descrita na equação 6.30, e o momento M é distribuído na seção transversal como mostra a Figura 6.54e. Prove que a tensão de cisalhamento máxima desenvolvida na viga é dada por τ m á x = 3 / 2 ( P / A ' ) , onde A ' = 2 y ' b , a área da seção transversal do núcleo elástico.

Passo 1

Em questões de cisalhamento elástico-plástico, o modus operandi é simplesmente ignorar a região plástica.

Vamos começar calculando o momento de inércia da região elástica:

I = 1 12 ⋅ b ( 2 y ) 3

I = 2 3 b y 3

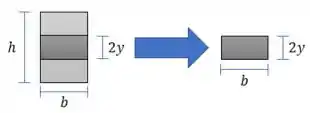
Passo 2

E calculamos o momento estático da região elástica

Q = b y ⋅ y 2

Q = b y 2 2

Passo 3

Agora aplicamos na equação do cisalhamento:

τ = V Q I t

τ = V ⋅ b y 2 2 2 3 b y 3 ⋅ b

τ = 3 V 4 b y

Perceba duas coisas, a primeira é que a força de cisalhamento é igual a P para qualquer ponto da viga. E segundo que 2 b y é igual a área A da região elástica

τ = 3 P 2 A

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura.
A força P é aplicada à alma da viga como mostra a figura. Se e = 250 m m , determine a altura h da aba direita de modo que a viga sofra deflexão para baixo sem torção. Os segmentos do elemento têm a m
A viga é composta por quatro tábuas pregadas como ostra a figura. Determine a força de cisalhamento à qual cada prego ao longo dos lados C e da parte superior D deve resistir se estiverem uniformement
Se a viga T for submetida a um cisalhamento vertical V=60kN, determine a tensão de cisalhamento máxima na viga. Calcule também o salto da tensão de cisalhamento na junção aba-alma AB. Trave um rascunh
Se o tubo estiver sujeito a um cisalhamento V = 75k N , determine a tensão de cisalhamento máxima nele.