Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 90
Os elementos de um macaco de chão são mostrados na figura. A figura é um paralelogramo. Calcule a força no cilindro hidráulico correspondente à carga de suportada, conforme mostrado. Qual é a força no link ?
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força no cilindro hidráulico devido ao carregamento de aplicado e a força na ligação .
Então bora resolver! Vamos começar analisando o diagrama de corpo livre do membro separadamente.
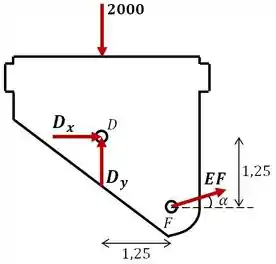
Uma vez que a estrutura está em equilíbrio, os membros separadamente também devem estar. Logo podemos fazer o equilíbrio de momentos em torno de para encontrar a reação .
Se a gente observar o diagrama de corpo livre, esse resultado já era previsto, pois o ponto faz parte da linha de ação da força de , restando apenas a força para realizar momento em torno desse ponto. Então, pela condição de equilíbrio, deve ser realmente igual a zero.
Passo 2
Show! Com esse resultado, ainda analisando o elemento , podemos usar as equações de equilíbrio de forças nas direções e para descobrir as reações no apoio .
Passo 3
Tranquilinho né? Agora, seguindo o mesmo princípio, vamos analisar o membro :
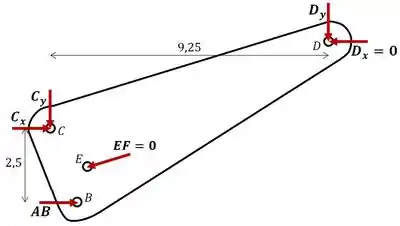
Novamente, pela condição de equilíbrio da estrutura, podemos usar o somatório de momentos em torno de algum ponto para descobrir . Como as reações do pino não são foco do nosso problema, vamos fazer o equilíbrio de momentos em torno deste ponto.
Ufa! Essa já foi hein? Partiu pra próxima!
