Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 44

A empilhadeira de 3   M g tem centro de massa em G . Determine o maior número de caixas que podem ser empurrados pela empilhadeira se cada caixa tem uma massa de 500 k g . O coeficiente de atrito estático entre uma empilhadeira e o solo é μ s = 0,3 , e o coeficiente de atrito estático entre as rodas traseiras da empilhadeira e o solo é μ s ' = 0,5 . As rodas da frente são livres para rolar. Assuma que o motor da empilhadeira seja poderoso o bastante para gerar um torque que faça as rodas traseiras deslizarem.

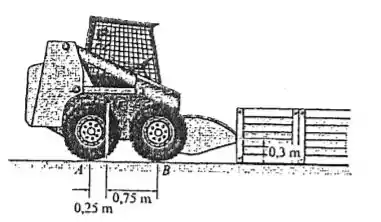
Passo 1

Queremos determinar o maior número de caixas que podem ser empurradas pela empilhadeira dadas as condições relatadas no problema. Tomemos, primeiramente, os seguintes diagramas de corpo livre referentes à empilhadeira e a caixa, respectivamente:

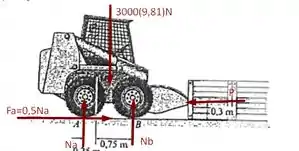
Passo 2

Com os diagramas de forças acima, podemos utilizar as equações de equilíbrio para encontrarmos o valor de P e N a fazendo

∑ M b = 0 → P ⋅ 0,3 + 3000 ⋅ 9,81 ⋅ 0,75 - N a ⋅ 1 = 0         ( i )

∑ F x = 0 → 0,5 ⋅ N a - P = 0             ( i i )

Resolvendo o sistema composto pelas equações i   e   ( i i ) encontramos

P = 12983,82 N   e   N a = 25967,65 N

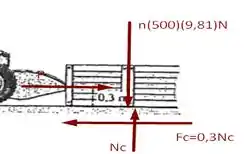
Passo 3

Tomando, agora, o diagrama de forças para o diagrama de corpo livre da caixa vamos ter

∑ F y = 0 → N c - n ⋅ 500 ⋅ 9,81 = 0 → N c = 4905 n

∑ F x = 0   → 12983,82 - 0,3 ⋅ 4905 n = 0 → n ≈ 8,8

∴ o   n ú m e r o   m á x i m o   d e   c a i x a s   q u e   p o d e m   s e r   e m p u r r a d a s   p e l a   e m p i l h a d e i r a   é   8

Resposta

8   c a i x a s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os blocos A e B têm massas de 7k g e 10k g , respectivamente. Usando os coeficientes de atrito estático indicados, determine a maior força P que pode ser aplicada à corda sem causar movimento. Há poli
Se o coeficiente de atrito estático em todas as superfícies de contato for u , determine a inclinação θ em que os blocos idênticos, de peso W cada um, começam a deslizar.
Os blocos A, B e C possuem pesos de 50N , 25N e 15N , respectivamente. Determine a menor força horizontal P que causará iminência de movimento. O coeficiente de atrito estático entre A e B é u s=0,3 ,
O came está sujeito a um momento de binário de 5N m . Determine a força mínima P que deverá ser aplicada ao seguidor para manter o came na posição mostrada. O coeficiente de atrito estático entre o ca
A  escada uniforme de  10 kg  se  apoia no piso  áspero para o qual o coeficiente de atrito estático é  u s=   0,4  e contra a parede lisa em B. Determine a força horizontal P que o homem precisa exer