Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 4
A empilhadeira tem peso de 12 kN e centro de gravidade em G. Se as rodas traseiras são tracionadas, enquanto as dianteiras estão livres para rodar, determine o número máximo de caixas de 150 kg que a empilhadeira pode empurrar para a frente. O coeficiente de atrito estático entre as rodas e o solo é , e entre cada caixa e o solo é .
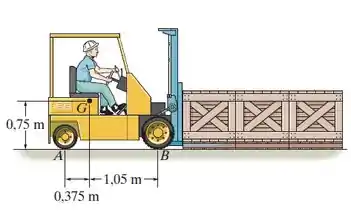
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos calcular o número máximo de caixas de 150 kg que a empilhadeira consegue empurrar. Ela será máxima quando a força de atrito na roda traseira for igual a força de atrito nas caixas.
Como a roda gira no sentido horário, a força de atrito na roda apontará para a direita (a favor do movimento do carro. Esboçando tudo isto no diagrama de corpo livre, temos:
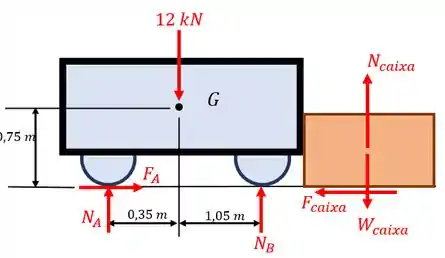
Antes de partirmos para o cálculo, vamos destrinchar alguns termos do enunciado. A força de atrito nas rodas traseiras são:
Já a força de atrito na caixa será:
Bom, agora que a gente já sabe todas as relações, vamos para as contas!
Passo 2
Antes que a gente possa descobrir quem é o número de caixas, precisamos descobrir qual o valor das forças normais em e em (na empilhadeira).
E isto é bem simples. Basta esquecermos que existe todas as outras forças e olhar apenas para a empilhadeira. Fazendo isto e aplicando as equações de equilíbrio para ela, temos
Portanto, do sistema acima nós obtemos:
Passo 3
Agora é só analisarmos o nosso sistema como um todo! Pela equação que escrevemos no Passo 1, a força de atrito nas rodas traseiras é:
Aplicando as equações de equilíbrio para o nosso sistema, temos:
Mas, como , temos:
E calculando o número de caixas que equivalem a este peso, temos:
E assim chegamos ao resultado final da nossa questão, 7 caixas!