Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 6
Determine o ângulo no qual a força aplicada deverá atuar sobre o tubo de modo que a intensidade de seja a menor possível para puxá-lo rampa acima. Qual é o valor correspondente de ? O tubo pesa e a inclinação é conhecida. Expresse a resposta em termos do ângulo de atrito cinético, .
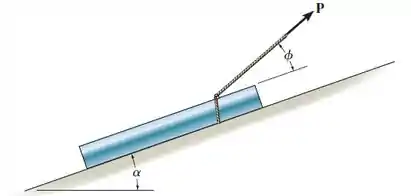
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta questão é uma continuação da questão 8.5. Portanto, vamos utilizar a relação da força que lá desenvolvemos. Relembrando, temos:
Com esta relação devemos descobrir qual o valor de para que a força seja a menor possível que puxa o tubo rampa acima e depois qual o valor desta força .
Bom, se lembrarmos lá de Cálculo 1, o ponto mínimo de uma função ocorre quando a sua derivada é nula. Portanto, o valor de tal que é mínimo é obtido quando
Agora que já sabemos o que fazer, vamos aos cálculos!
Passo 2
Agora vamos ter que derivar a nossa função e igualar ela a zero. Portanto,
E assim resolvemos a primeira parte da questão!
Passo 3
Para finalizarmos a questão, temos que calcular o valor de quando . Portanto,
E assim finalizamos a questão!