Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 46
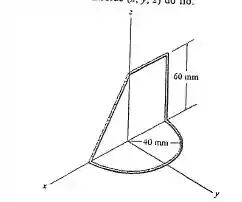
Encontre o centroide do fio.
Passo 1
Fala, galerinha! Como temos um fio composto por outras formas mais simples e conhecidas, vamos dividir o fio em partes, achar o centro de massa de cada uma e depois usar a fórmula do centroide para regiões compostas! Bora lá!
Para cada forma a gente vai listar o comprimento, e as coordenadas do centroide.
Vamos começar olhando a semicírcunferência. O centroide dela é distante do seu centro. Como ela é simétrica em relação a , a coordenada do centroide é zero
E como ela está contida no plano , o centroide dela está nesse plano, então a coordenada também vai ser zero:
E na coordenada , usamos a informação de que o centoide é distante do centro. Isso porque o centro está contido nesse eixo.
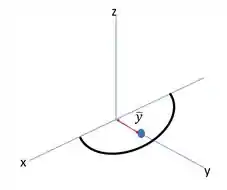
Já que o centro é a origem dos sistema de coordenadas, temos então que
E o comprimento dessa semicircunferência vai ser
Passo 2
Vamos para as barrinhas horizontais e verticais. O centroide delas vai ser no meio de cada uma. Levando em consideração que podemos desconsiderar que elas tem espessura, e olhando nossa figurinha, podemos dizer que
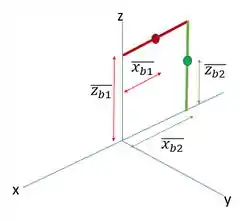
Repara que o de e o de ficaram negativo, porque eles estão na parte negativa de .
Passo 3
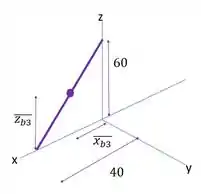
Para finailizar, o centroide da barra inclinada também é no meio dela. E é importante perceber que a gente vai usar pitagoras para achar seu comprimento. Fica assim:
Passo 4
Vamos fazer no modelo de tabela com as posições que achamos que fica melhor pra gente visualizar.
Agora, tendo todas as coordenadas do centro de massa, podemos aplicar a fórmula do centroide!