Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 37
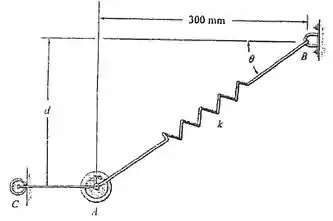
3.37. O peso de é suportado pela corda AC, pelo rolete, e por uma mola que possui uma rigidez de e um comprimento não deformado de 300 mm. Determine a distância d até onde o peso está localizado quando em equilíbrio.
Passo 1
Fala, meu querido! Queremos o valor de . Nós podemos extrair esse triângulo do exercício
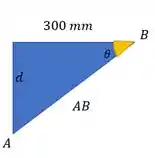
Podemos achar então pela relação trigonométrica:
Mas a gente precisa encontrar . Como ele diz que tudo está em equilíbrio, a gente pode calcular as resultantes nos eixos coordenados e igualar a zero. Aí achamos .
Mas lembra: falou de usar equações de equilíbrio, vamos fazer o DCL:
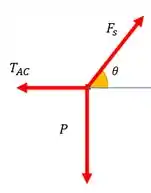
Bora!
Passo 2
Vamos usar as equações de equilíbrio
Então
E para o eixo y temos
Lembra de multiplicar pela massa e achar o peso em A.
Passo 3
Agora a força da mola pode ser definida como
Esse é o quanto a mola deformou. A gente pode acha-lo fazendo a diferença entre o comprimento não deformado da mola, , e o comprimento da mola no nosso problema, que é .
Para achar , vamos usar o triângulo do passo 1, e escrever esse segmento em função de Nele vemos que:
A deformação fica:
Então
Passo 4
Substituindo nas equações temos
Então temos
Essa equação a gente vai resolver numa calculadora de expressões, tá? Porque a mão é complicado, é necessário usar algum método matemático para chegar no valor.
Aí a gente acha:
Passo 5
Do triângulo extraído do exercício podemos dizer que
Prontinho!