Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 169
Encontre o comprimento total L da corrente que terá uma curvatura de 6 pés quando suspensa em dois pontos na mesma linha horizontal a 30 pés de distância.
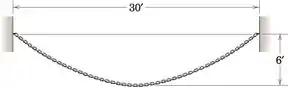
Passo 1
No esboço abaixo, podemos ver que ambas as extremidades do cabo estão na mesma altura, o que significa que o ponto mais baixo (início do nosso sistema de coordenadas) está no meio da cadeia. Sabendo disso, podemos dizer que as coordenadas do ponto A são
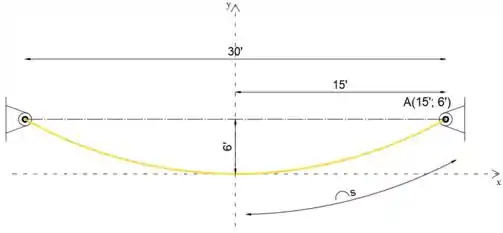
Em seguida, como o cabo suporta apenas seu peso, o cabo tem uma forma conhecida como catanaria, portanto, para determinar o comprimento do cabo (2s), usaremos a expressão (5/20)
Substitua x pela coordenada do ponto A
Passo 2
Observe que T0 e são desconhecidos, bem como a razão T0/, que podemos determinar a partir da expressão (5/19)
Coloque as coordenadas do ponto A na equação
Passo 3
Usando uma calculadora gráfica como o Desmos (link nos comentários), vamos representar graficamente a função e ler o valor de em
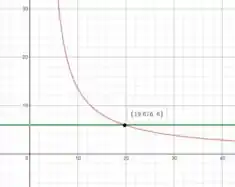
Finalmente, vamos substituir por seu valor na equação (1)
Percebemos que o comprimento do cabo é