Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 173
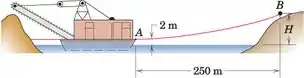
Uma draga flutuante é ancorada em posição com um único cabo de popa que tem uma direção horizontal no anexo A e se estende por uma distância horizontal de 250 m até uma ancoragem B na costa. Uma tensão de 300 kN é necessária no cabo em A. Se o cabo tiver uma massa de 22 kg por metro de seu comprimento, calcule a altura H necessária da ancoragem acima do nível da água e encontre o comprimento s do cabo entre A e B .
Passo 1
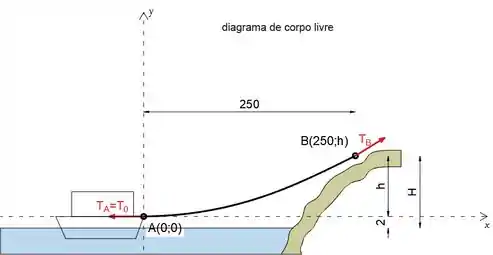
Primeiro, vamos desenhar o diagrama de corpo livre do cabo.
Observe que, uma vez que o cabo suporta apenas seu peso, o cabo tem uma forma conhecida como catenária
Como o cabo é horizontal em A, sabemos que a tensão TA é horizontal, ou seja, é igual a T0
O peso por metro de comprimento é igual à massa por comprimento vezes a gravidade:
Passo 2
Também podemos ver no esboço que o início do sistema de coordenadas está 2 m acima da água, então podemos escrever a distância H como:
Observe que a função do cabo é:
Substitua T0 e por seus valores e coloque as coordenadas do ponto B na equação
Passo 3
Usando uma calculadora gráfica como o Desmas (link nos comentários), traçaremos a função e e leremos a solução do ponto de intersecção
Substitua T0 por seu valor na expressão (1)
A seguir, usando a expressão (5/20), podemos determinar o comprimento do cabo
Substitua T0 e m por seus valores e x pela coordenada do ponto B, uma vez que o ponto A está no início do sistema de coordenadas