Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 110
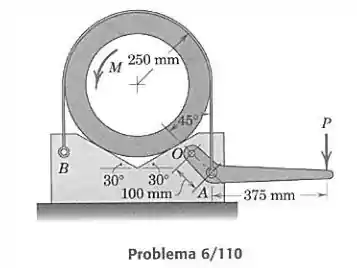
Encontre o momento necessário para girar o tubo no bloco em V contra a ação da cinta flexível, no projeto do freio de cinta mostrado. Uma força é aplicada à alavanca, que pivota em torno de . O coeficiente de atrito entre a cinta e o tubo vale 0,30 e entre o tubo e o bloco vale 0,40. Os pesos das peças são desprezíveis.
Passo 1
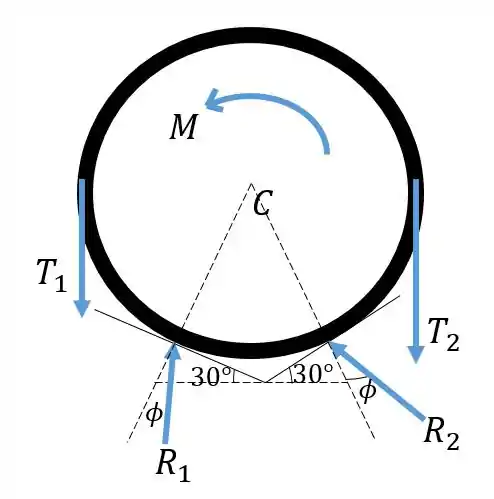
Vamos primeiro representar o tubo e o trecho da cinta que está colada nele em um diagrama de corpo livre. Atuam sobre o corpo trações e nas partes onde a cinta se desencosta, as forças e feitas pelo bloco nos dois pontos de contato e o momento . O ângulo entre as forças e e a linha normal à superfície de contato deve ser , tal que , pois esse é o coeficiente de atrito entre o bloco e o tubo. Além disso, e devem se posicionar de modo que a componente tangente ao tubo (o atrito) esteja contrária à tendência ao giro causada por :
Passo 2
Primeiro vamos encontrar a tração , através do momento em torno de na alavanca. A distância horizontal entre e é , e a distância horizontal entre a aplicação de e é . Então:
Como :
Passo 3
Agora achamos através da fórmula do equilíbrio da cinta enrolada no tubo. A fórmula é a seguinte:
Sendo o ângulo total do enrolamento da cinta, que é (meia volta) e o coeficiente de atrito entre a cinta e o tubo. Então:
Usamos o valor de encontrado anteriormente e determinamos :
Passo 4
Agora temos só três incógnitas para as forças no tubo: e . Então conseguimos resolver com duas equações de força e uma de momento. Vamos primeiro determinar o ângulo :
As inclinações de e em relação à horizontal são e , respectivamente, como mostra a figura:
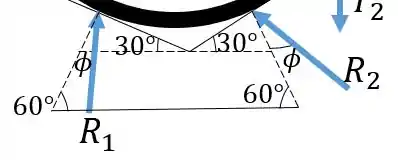
Então vamos às equações. Primeiro para a direção horizontal :
Agora a soma das forças na direção vertical :
Substituímos os valores de e e trocamos por :
Então achamos também :
Passo 5
Agora que temos os valores de todas as forças, fazemos o momento em torno do centro ser zero para encontrar . O raio do tubo é 0,25 m, e as componentes das forças e que causam momento são as tangentes ao tubo, e :