Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 123
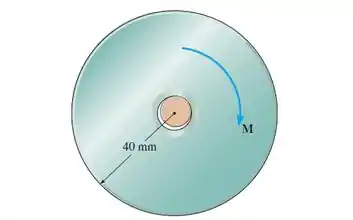
Uma polia com 80 mm de diâmetro e 1,25 kg de massa é suportada livremente em um eixo com 20 mm de diâmetro. Determine o torque que deverá ser aplicado à polia para fazer com que ela gire com movimento constante. O coeficiente de atrito cinético entre o eixo e a polia é . Além disso, calcule o ângulo que a força normal no ponto de contato faz com a horizontal. O próprio eixo não poderá girar.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos aqui um caso de mancal radial de deslizamento. Para esta questão, o nosso objetivo é determinar o torque que deve ser aplicado na polia para que ela rotacione com velocidade constante e também determinar o ângulo que a força normal faz com a horizontal.
Bom, a polia gira com velocidade constante quando o torque se iguala ao momento gerado pelo peso.
Para este caso, o momento do peso será dado por:
Com . Então, o momento será:
E assim calculamos o valor do torque !
Passo 2
Para finalizarmos a questão nós precisamos calcular o ângulo que faz com a direção horizontal. E aqui é bem simples, pois este ângulo é exatamente:
E assim nós finalizamos a questão!