Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 121
Resolva o Problema 8.120 se a força for aplicada horizontalmente à esquerda.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta questão é exatamente o problema 8.120, só que com a força na horizontal.
Sendo assim, o nosso objetivo é calcular a força quando a mesma está na horizontal.
Esboçando o diagrama de corpo livre, temos:
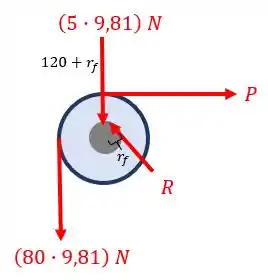
Com posse deste diagrama, vamos as contas!
Passo 2
O nosso primeiro passo é determinar a distância . Aqui é basicamente aplicação direto da fórmula.
Portanto,
Passo 3
Continuando, para que a gente descubra qual o valor de , vamos ter que aplicar as equações de equilíbrio.
Então, vamos começar devagar. Primeiro vamos correlacionar a reação com as forças na polia. Separando nas componentes horizontal e vertical, temos:
E assim chegamos, a partir das duas primeiras equações, que e . Só que da terceira equação nós temos que .
E agora??? Simples! Precisamos correlacionar as três informações! Por definição, a força é:
Logo,
Resolvendo esta equação obtemos .
E assim finalizarmos a questão!