Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 90

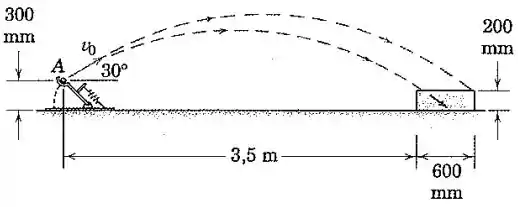
Uma equipe de estudantes de engenharia está projetando uma catapulta para lançar uma pequena bola em A de modo que esta caia na caixa. Sabendo que o vetor velocidade inicial faz um ângulo de 30 ° com a horizontal, determine a faixa de velocidades de lançamento v 0 com a qual a bola cairá dentro da caixa.

Passo 1

Galera, pra determinar a faixa de velocidades de lançamento com a qual a bola cai dentro da caixa, a gente precisa escrever a equação da trajetória parabólica da bola, a fim de que tenhamos 3,5   m ≤ x ≤ 3,5   m + 600   m m quando y = 200   m m , beleza?

Então, vamos começar equacionando o movimento horizontal:

x = v x t = v 0 cos ⁡ 30 ° t

t = x v 0 cos ⁡ 30 °

t = 1,15 x v 0

Para o movimento vertical, considere y 0 = 300   m m = 0,3   m :

y = y 0 + v 0 y t - 1 2 g t 2 = 0,3 + v 0   s e n   30 ° t - 1 2 g t 2 = 0,3 + 0,5 v 0 t - 4,9 t 2

Substituiremos a expressão de t encontrada:

y = 0,3 + 0,5 v 0 1,15 x v 0 - 4,9 1,15 x v 0 2

y = 0,3 + 0,575 x - 6,48 v 0 2 x 2

Passo 2

Com a equação trajetória encontrada, podemos substituir os dois valores limites de x para y = 200   m m = 0,2   m . Se x = 3,5   m , temos:

0,2 = 0,3 + 0,575 3,5 - 6,48 v 0 2 3,5 2

79,4 v 0 2 = 2,11

v 0 = 6,1   m / s

Mas, se x = 3,5   m + 600   m m = 4,1   m , teremos:

0,2 = 0,3 + 0,575 4,1 - 6,48 v 0 2 4,1 2

109 v 0 2 = 2,46

v 0 = 6,7   m / s

Logo, devemos ter a seguinte faixa de velocidades:

6,1   m / s ≤ v 0 ≤ 6,7   m / s

Resposta

6,1   m / s ≤ v 0 ≤ 6,7   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um projétil é lançado a partir do ponto A com as condições iniciais mostradas na figura. Determine as coordenadas x e y do ponto de impacto.
Um projétil é lançado em um fluido experimental no instante t = 0 . A velocidade inicial é v 0 e o ângulo com a horizontal é θ . O arrasto sobre o projétil resulta em um termo de aceleração a D = - k
Um projétil é lançado a partir do ponto A e cai no mesmo nível em D . Sua altitude máxima é h . Determine e represente graficamente a fração f 2 do tempo total de voo em que o projétil está acima do n
Uma bola é jogada para cima com uma velocidade de 5 m/s do topo de um prédio de 10 m de altura. Um segundo mais tarde, outra bola é jogada verticalmente a partir do chão com uma velocidade de 10 m/s.
Uma partícula move-se ao longo de uma curva definida pela equação s=( t ³-3 t ²+2 t ) ³ ² m, onde t é dado em segundos. Trace os gráficos s - t ,v - t e a - t para a partícula em 0≤t≤3 s .