Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 95

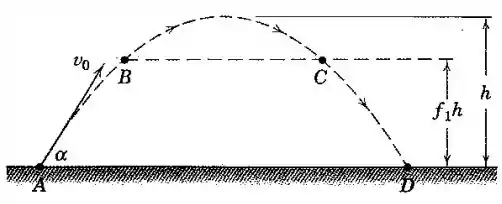
Um projétil é lançado a partir do ponto A e cai no mesmo nível em D . Sua altitude máxima é h . Determine e represente graficamente a fração f 2 do tempo total de voo em que o projétil está acima do nível f 1 h , onde f 1 é uma fração que pode variar de zero a 1 . Expresse o valor de f 2 para f 1 = 3 4 .

Passo 1

Galera, vamos escrever a fração f 2 assim:

f 2 = t 1 T

onde t 1 é o tempo que o projétil passa acima do nível f 1 h e T é o tempo total de voo.

Podemos analisar apenas metade do movimento, até a altura máxima h , por causa da sua simetria.

Então, primeiro vamos calcular o tempo T até o projétil atingir a altura máxima, onde tem velocidade nula, por meio da equação:

v y = v 0 y - g t

0 = v 0   s e n   α - g T

T = v 0   s e n   α g

Passo 2

Show! Agora vamos tentar calcular o valor de t ' = T - t 1 , equivalente ao tempo que o projétil demora para alcançar a altura f 1 h (ou seja, o tempo abaixo do nível f 1 h ):

y = v 0 y t - 1 2 g t 2

f 1 h = v 0   s e n   α   t ' - 1 2 g t ' 2

Antes de isolar t ' nessa equação, vamos usar mais uma equação que pode nos dar uma relação útil para h :

v y 2 = v 0 y 2 - 2 g y

0 2 = v 0   s e n   α 2 - 2 g h

v 0   s e n   α = 2 g h

Passo 3

Usamos a última equação obtida para substituir a expressão de v 0   s e n   α na equação de t ' :

f 1 h = v 0   s e n   α   t ' - 1 2 g t ' 2

f 1 h = 2 g h   t ' - 1 2 g t ' 2

g t ' 2 - 2 2 g h   t ' + 2 f 1 h = 0

Por fim, resolvemos a equação quadrática:

Δ = 2 2 g h 2 - 4 g 2 f 1 h = 8 g h - 8 f 1 g h = 8 g h 1 - f 1

t ' = 2 2 g h ± 8 g h 1 - f 1 2 g = 2 g h ± 2 g h 1 - f 1 g = 2 g h g 1 ± 1 - f 1

t ' = 2 h g 1 - 1 - f 1

Consideramos somente a menor solução pois estamos procurando o tempo t ' na primeira metade da parábola.

Passo 4

Agora podemos enfim expressão f 2 somente em função de f 1 , veja a mágica acontecer:

f 2 = t 1 T = T - t ' T = 1 - t ' T

f 2 = 1 - 2 h g 1 - 1 - f 1 v 0   s e n   α g = 1 - 2 h g 1 - 1 - f 1 2 g h g = 1 - 2 h g 1 - 1 - f 1 2 h g

f 2 = 1 - 1 - 1 - f 1

f 2 = 1 - f 1

Beleza?

Passo 5

Agora vamos representar nossa solução por meio de um gráfico, com f 2 no eixo y e f 1 no eixo x :

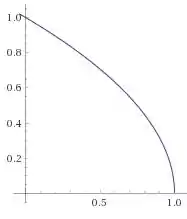
E por último, obter f 2 para f 1 = 3 4 :

f 2 = 1 - f 1 = 1 - 3 4

f 2 = 1 2

Resposta

f 2 = 1 - f 1

f 2 = 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A plataforma está girando em torno do eixo vertical de modo que em qualquer instante a sua posição angular é θ = ( 4 t 3 / 2 ) , onde t é dado em segundos. Uma bola rola para fora ao longo do sulco ra
Na parte baixa do loop em um plano vertical, um aeroplano tem velocidade de 150 m/s e está acelerando a uma taxa de 25 m/s2. O raio de curvatura do loop é 2.000 m. O aeroplano está sendo controlado pe
A partir de medições de uma fotografia, verificou-se que o fluxo de água mostrado na figura deixa o bocal em A e tem raio de curvatura de 25 m. Determine (a) a velocidade inicial vA do fluxo, (b) o ra
Um morador usa o removedor de neve para limpar a entrada de sua garagem. Sabendo que a neve é lançada a um ângulo médio de 40° com a horizontal, determine a velocidade inicial v0 da neve.
Um projétil é disparado com velocidade inicial v 0 em um ângulo de elevação α para cima de uma colina com inclinação β ( αβ ) (a) Qual será a distância de aterrissagem do projétil colina acima? (b) Em