Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 49
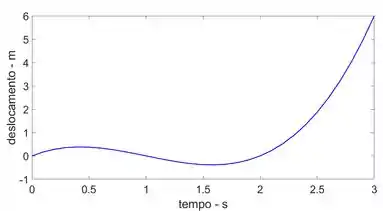
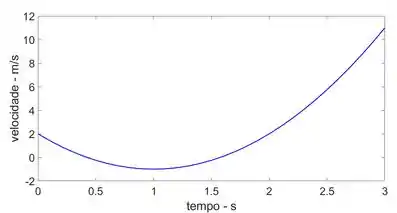
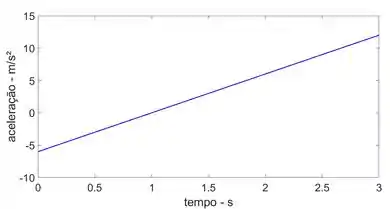
Uma partícula move-se ao longo de uma curva definida pela equação m, onde t é dado em segundos. Trace os gráficos , e para a partícula em .
Passo 1
Sabendo que a velocidade é a derivada do deslocamento e a aceleração é a derivada da velocidade, ambos no tempo,
Passo 2
Aplicando ao problema,
Passo 3
Num é nem um passo, é só um comentário. Nesse momento a idéia seria calcular , e para vários instantes e desenhar os gráficos.
Resposta
Os gráficos s-t, v-t e a-t estão mostrados abaixo.
Exercícios de Livros Relacionados
Um projétil é disparado com velocidade v 0 de modo a passar entre dois pontos a uma distância h acima da horizontal. Mostre que, se a arma for ajustada para alcance máximo, a separação entre os pontos
Na nevasca de 88, uma fazendeira foi forçada a lançar fardos de feno de um avião para alimentar seu gado. A aeronave voou horizontalmente a 160k m / h e jogou os fardos de uma altura de 80m sobre a pa
Um piloto de jato sabe que é capaz de suportar uma aceleração de 9 g antes de perder os sentidos. Ele aponta sua aeronave verticalmente para baixo voando em velocidade Mach3 e pretende arremeter em um
Um palhaço faz malabarismo com quatro bolas simultaneamente. Os alunos utilizam uma gravação em vídeo para determinar que o palhaço leva 0,9s para trocar cada bola entre suas mãos (inclui pegar, trans
Inclua a resistência do ar para os fardos de feno no problema anterior. Um fardo de feno tem massa aproximada de 30k g e área de cerca de 0,2m 2 . Considere a resistência do ar proporcional ao quadrad