Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 97

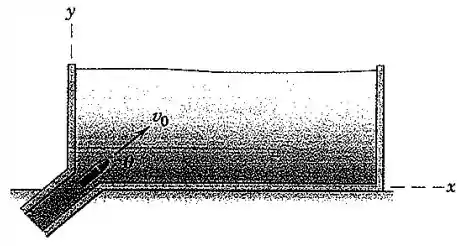
Um projétil é lançado em um fluido experimental no instante t = 0 . A velocidade inicial é v 0 e o ângulo com a horizontal é θ . O arrasto sobre o projétil resulta em um termo de aceleração a D = - k v , onde k é uma constante e v é a velocidade do projétil. Determine as componentes x e y da velocidade e do deslocamento como funções do tempo. Qual é a velocidade final? Inclua os efeitos da aceleração gravitacional.

Passo 1

Para o movimento horizontal, teremos:

a x = - k v x

Vamos usar a seguinte equação diferencial:

d v = a   d t

d v = - k v   d t

1 v   d v = - k   d t

Lembre-se que quando t = 0 , temos v x = v 0 cos ⁡ θ :

∫ v 0 cos ⁡ θ v x 1 v   d v = - k ∫ 0 t d t

ln ⁡ v x - ln ⁡ v 0 cos ⁡ θ = - k t

ln ⁡ v x v 0 cos ⁡ θ = - k t

v x v 0 cos ⁡ θ = e - k t

v x = v 0 cos ⁡ θ e - k t

Passo 2

Para descobrir o deslocamento x em função do tempo, usamos a velocidade v x que acabamos de obter na seguinte equação diferencial:

d x = v   d t

d x = v 0 cos ⁡ θ e - k t   d t

∫ 0 x d x = v 0 cos ⁡ θ ∫ 0 t e - k t d t

x = v 0 cos ⁡ θ - e - k t k 0 t

x = v 0 cos ⁡ θ k 1 - e - k t

Passo 3

Agora trataremos do movimento vertical:

a y = - k v y - g

Podemos usar a seguinte equação diferencial:

d v = a   d t

d v = - k v - g   d t

1 v + g / k   d v = - k   d t

Lembre-se que quando t = 0 , temos v y = v 0   s e n   θ :

∫ v 0   s e n   θ v y 1 v + g / k   d v = - k ∫ 0 t d t

ln ⁡ v y + g k - ln ⁡ v 0   s e n   θ + g k = - k t

ln ⁡ v y + g / k v 0   s e n   θ + g / k = - k t

v y + g / k v 0   s e n   θ + g / k = e - k t

v y = v 0   s e n   θ + g k e - k t - g k

Passo 4

Para descobrir o deslocamento y em função do tempo, usamos a velocidade v y que acabamos de obter na seguinte equação diferencial:

d y = v   d t

d y = v 0   s e n   θ + g k e - k t - g k   d t

∫ 0 y d y = ∫ 0 t v 0   s e n   θ + g k e - k t - g k d t

y = v 0   s e n   θ + g k - e - k t k - g k t   0 t

y = 1 k v 0   s e n   θ + g k 1 - e - t - g k t

Passo 5

Para calcular a velocidade final, vamos considerar cada componente da velocidade em particular, e tomar o seu limite quando t → ∞ :

v x = v 0 cos ⁡ θ e - k t

v x → 0

v y = v 0   s e n   θ + g k e - k t - g k

v y → - g k

Resposta

v x = v 0 cos ⁡ θ e - k t

x = v 0 cos ⁡ θ k 1 - e - k t

v y = v 0   s e n   θ + g k e - k t - g k

y = 1 k v 0   s e n   θ + g k 1 - e - t - g k t

v x → 0

v y → - g k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um míssil de dois estágios é lançado verticalmente a partir do repouso com a aceleração mostrada. Em 15 s, o primeiro estágio A esgota-se e o segundo estágio B dá partida. Elabore os gráficos v - t e
As cavilhas A e B estão restritas a moverem-se nas fendas elípticas devido ao movimento da fenda da barra. Se a fenda da barra se desloca com uma velocidade escalar constante de 10 m/s, determine a in
A cavilha P é inpulsionada pelo anel do garfo O A ao longo da trajetória curva descrita por r = ( 2 θ ) m. No instante θ = π / 4 rad, a velocidade angular e a aceleração angular do anel garfo são θ ˙
O carro tem uma velocidade escalar de 16.5 m/s. Determine a velocidade angular θ ˙ da linha radial O A nesse instante.
A cavilha P é inpulsionada pelo anel do garfo O A ao longo da trajetória curva descrita por r = e θ . Quando θ = π / 4 rad, o anel tem uma velocidade angular e a aceleração angular de θ ˙ = 2 rad/s e