Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 98
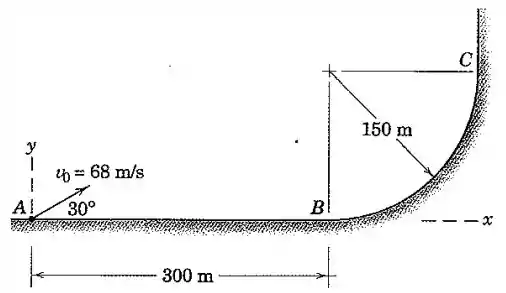
Um projétil é lançado a partir do ponto com as condições iniciais mostradas na figura. Determine as coordenadas e do ponto de impacto.
Passo 1
Pessoal, como estamos trabalhando aqui principalmente com as dimensões e , e não velocidades ou tempos, será bastante útil desenvolvermos a equação da trajetória do projétil, que nos dá justamente sua posição em função de sua posição .
Começamos pela seguinte equação do movimento horizontal:
Agora, a gente escreve a seguinte equação do movimento vertical:
Só resta substituir a expressão de já encontrada:
Nosso projétil é lançado da posição com velocidade e fazendo um ângulo com a horizontal, beleza? Vamos substituir esses valores na equação acima:
Então essa é a equação da trajetória, beleza?
Passo 2
Show! Como a gente quer as coordenadas do ponto de impacto, que provavelmente será em algum ponto do trajeto , podemos escrever uma equação de e que represente essa curva do trajeto.
Observe que é o quarto inferior direito de um círculo de raio . Então sua equação é assim:
onde são as coordenadas do centro do círculo, já que consideramos o ponto como a origem do nosso sistema de coordenadas quando fizemos .
Passo 3
Finalmente, para achar o ponto de impacto, vamos calcular a intersecção entre as duas curvas, da trajetória do projétil e do trajeto . Perceba que na equação da trajetória já temos isolado:
Substituímos isso na equação da circunferência e desenvolvemos:
Como o auxílio de um computador para resolver essa equação do quarto grau, obtemos:
Porém, devemos ter , então . Substituímos esse valor em :